Geração de Malha de Cilindros em Tandem Utilizando Gmsh
Geração de malha de cilindros em tandem utilizando Gmsh
Observações:
- Este tutorial tem função meramente didática, visando auxiliar usuários iniciantes, e não representa garantias de qualidade de resultados da simulação. A verificação e validação dos resultados, assim como estudos de refino de malha e demais análises, são de responsabilidade do usuário final.
- This offering is not approved or endorsed by OpenCFD Limited, producer and distributor of the OpenFOAM software via www.openfoam.com, and owner of the OPENFOAM® and OpenCFD® trade marks.
- Este tutorial foi criado dentro do contexto de um projeto de extensão da UFSC e não é homologado pelos desenvolvedores dos códigos GMSH e OpenFOAM®.
- Este tutorial foi elaborado pelo aluno de graduação Julio Victor Vieira e Widmark Kauê Silva Cardoso, sob supervisão de Filipe Dutra da Silva.
- Ao utilizar este material, solicita-se que sejam dadas as devidas referências à esta página. Dúvidas e sugestões podem ser enviadas aos endereços de contato da página.
Este tutorial apresenta os procedimentos para a geração de uma malha estruturada de cilindros em tandem utilizando o Gmsh. Serão apresentados tanto os passos para gerar a malha pela interface gráfica quanto pelo script.
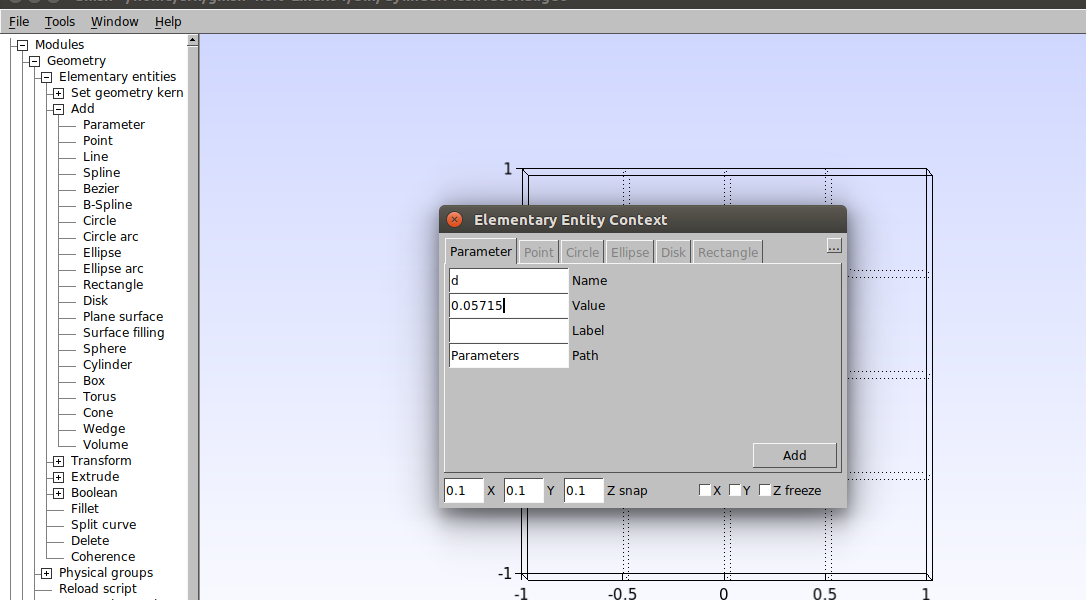
Primeiramente vamos definir os parâmetros que serão úteis ao longo do processo. Com o Gmsh aberto clique em Modules→Geometry→Elementary Entities → Add → Parameter. Na janela que abrir, defina o valor do diâmetro dos cilindros como sendo 0.05715 e clique em “Add”, conforme mostrado na figura abaixo.
Antes de fechar essa janela, adicione um novo parâmetro com o nome “cos” e valor de 0.70710678 que é o valor do cos 45° em radianos. Clique em “Add” e feche a janela.
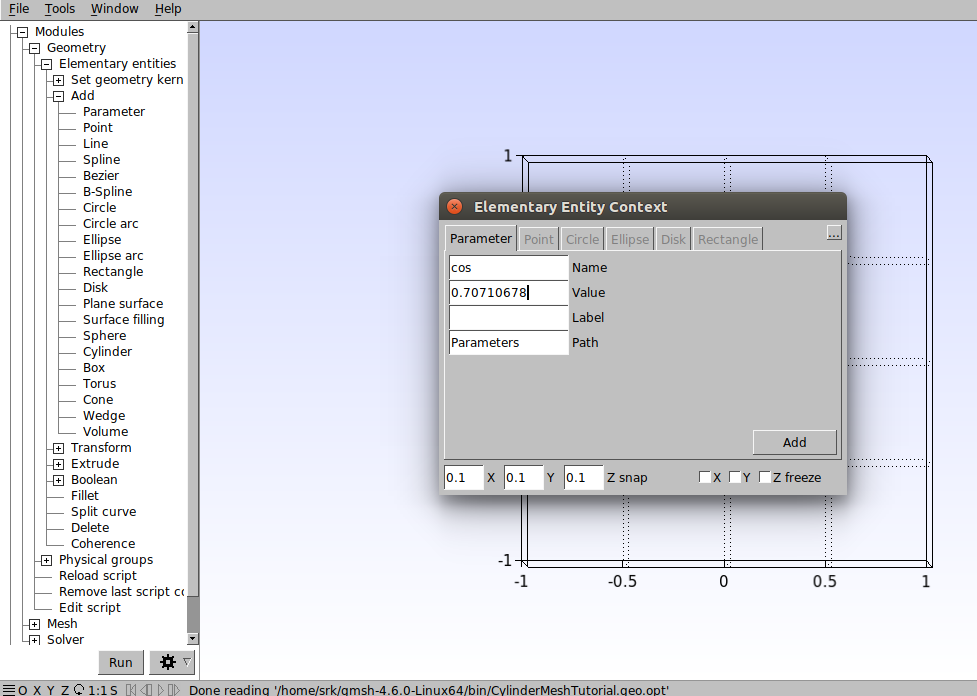
Para criar os parâmetros pelo script clique em Modules→Geometry→Edit script. No editor de texto que abrir devem ser inseridos os seguintes comandos:
// Parâmetros
d = DefineNumber[ 0.05715, Name "Parameters/d" ];
//+
cos = DefineNumber[ 0.70710678, Name "Parameters/cos" ];
Vamos agora definir os pontos necessários para construir os cilindros e também o domínio da simulação. No editor de texto, começamos inserindo o centro de cada cilindro e em seguida os pontos que os definem, como mostrado abaixo. É importante prestar atenção à numeração de cada ponto, pois atribuir um mesmo número a dois pontos diferentes ocasionará erros.
// Centro do cilindro 1
Point(1) = {0, 0, 0, 1.0};
// Centro do cilindro 2
Point(2) = {3.7*d, 0, 0, 1.0};
// Pontos que definem o cilindro 1
Point(3) = {cos*d/2, cos*d/2, 0, 1.0};
Point(4) = {-cos*d/2, cos*d/2, 0, 1.0};
Point(5) = {-cos*d/2, -cos*d/2, 0, 1.0};
Point(6) = {cos*d/2, -cos*d/2, 0, 1.0};
// Pontos que definem o cilindro 2 Point(7) = {cos*d/2 + 3.7*d, cos*d/2, 0, 1.0}; Point(8) = {-cos*d/2 + 3.7*d, cos*d/2, 0, 1.0}; Point(9) = {-cos*d/2 + 3.7*d, -cos*d/2, 0, 1.0}; Point(10) = {cos*d/2 + 3.7*d, -cos*d/2, 0, 1.0};Salve o script e vá para o Gmsh, e então clique em Modules→Geometry→Reload script para aplicar as alterações feitas no editor de texto (esse procedimento deve ser repetido sempre que você modificar o script no editor de texto). O resultado dessas configurações deve ser o seguinte:
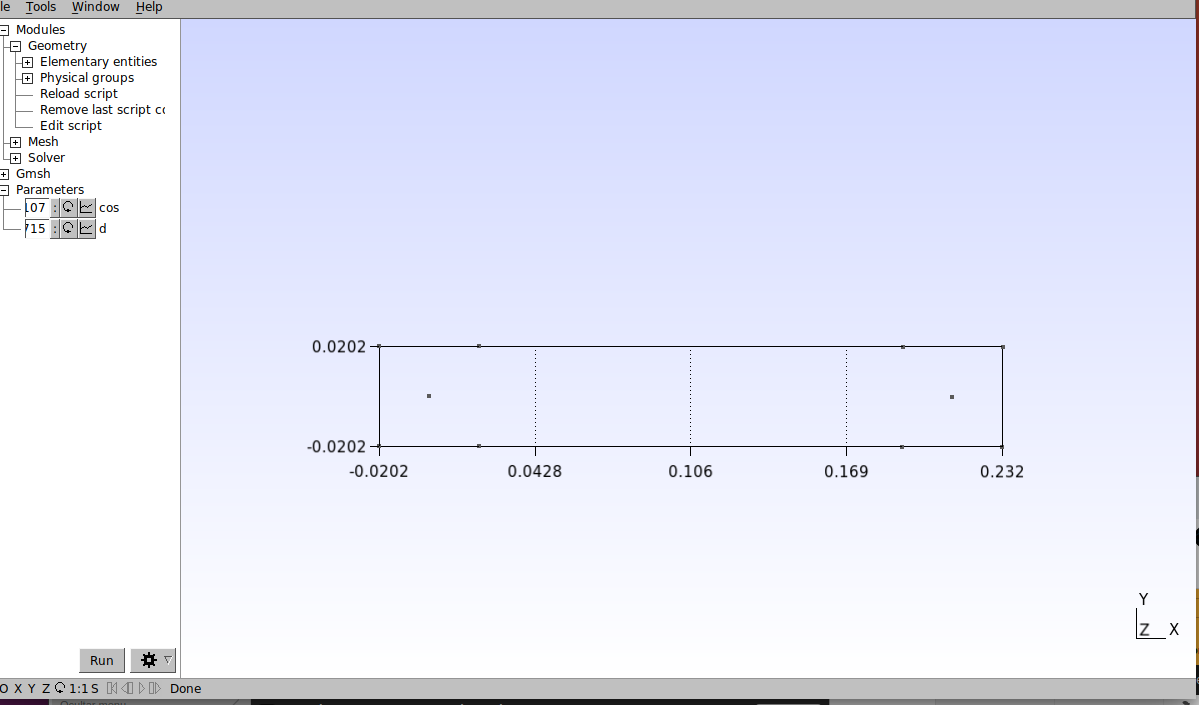
Vamos, agora, definir os limites do domínio. Abra o editor de texto e defina os seguintes pontos:
// Pontos que definem os limites do domínio
Point(11) = {-0.75, 0.75, 0, 1.0};
Point(12) = {-0.75, -0.75, 0, 1.0};
Point(13) = {2, 0.75, 0, 1.0};
Point(14) = {2, -0.75, 0, 1.0};
Salve e recarregue o script. O resultado deve ser o seguinte.
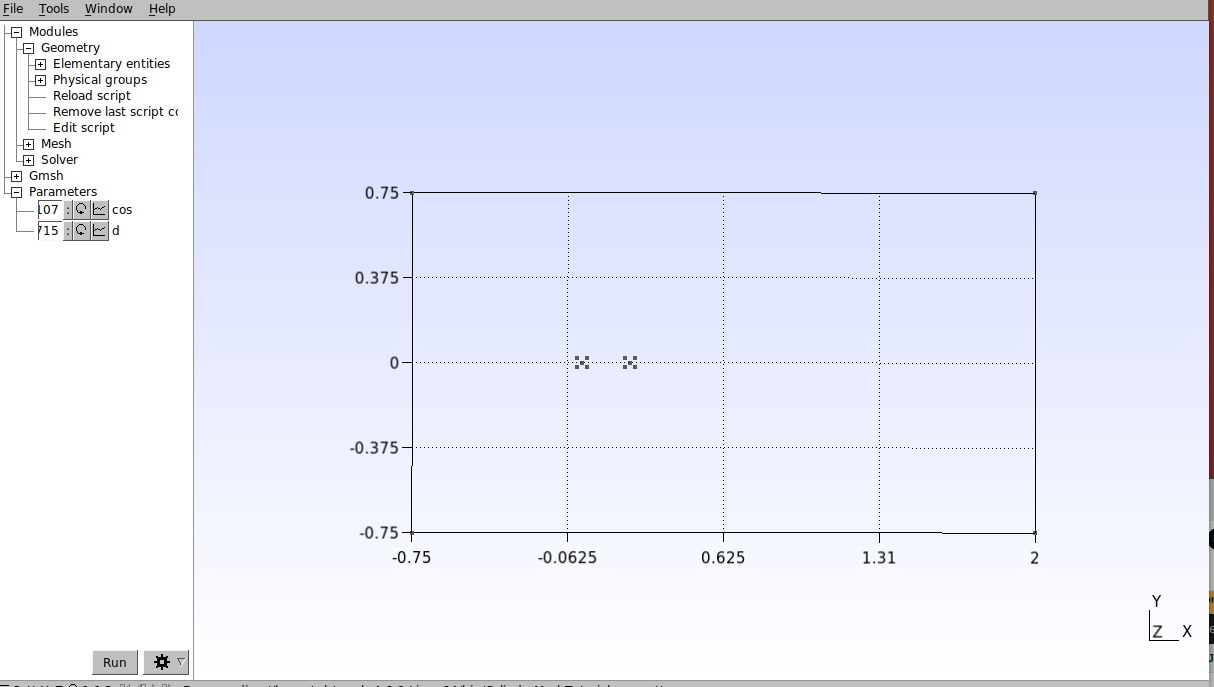
Em seguida, vamos definir o conjunto de pontos necessários para fazer a divisão do domínio. Isso é importante para as próximas etapas em que faremos o refino da malha. No editor de texto, insira os seguintes pontos:
// Pontos para a partição do domínio
Point(15) = {3.7*d/2, 3.7*d/2, 0, 1.0};
Point(16) = {3.7*d/2, -3.7*d/2, 0, 1.0};
Point(17) = {-3.7*d/2, 3.7*d/2, 0, 1.0};
Point(18) = {-3.7*d/2, -3.7*d/2, 0, 1.0};
Point(19) = {3.7*d/2 + 3.7*d, 3.7*d/2, 0, 1.0};
Point(20) = {3.7*d/2 + 3.7*d, -3.7*d/2, 0, 1.0};
Point(21) = {-0.75, 3.7*d/2, 0, 1.0};
Point(22) = {-0.75, -3.7*d/2, 0, 1.0};
Point(23) = {2, 3.7*d/2, 0, 1.0};
Point(24) = {2, -3.7*d/2, 0, 1.0};
Point(25) = {3.7*d/2, 0.75, 0, 1.0};
Point(26) = {3.7*d/2, -0.75, 0, 1.0};
Point(27) = {-3.7*d/2, 0.75, 0, 1.0};
Point(28) = {-3.7*d/2, -0.75, 0, 1.0};
Point(29) = {3.7*d/2 + 3.7*d, 0.75, 0, 1.0};
Point(30) = {3.7*d/2 + 3.7*d, -0.75, 0, 1.0};
O resultado deve ser como o mostrado abaixo:
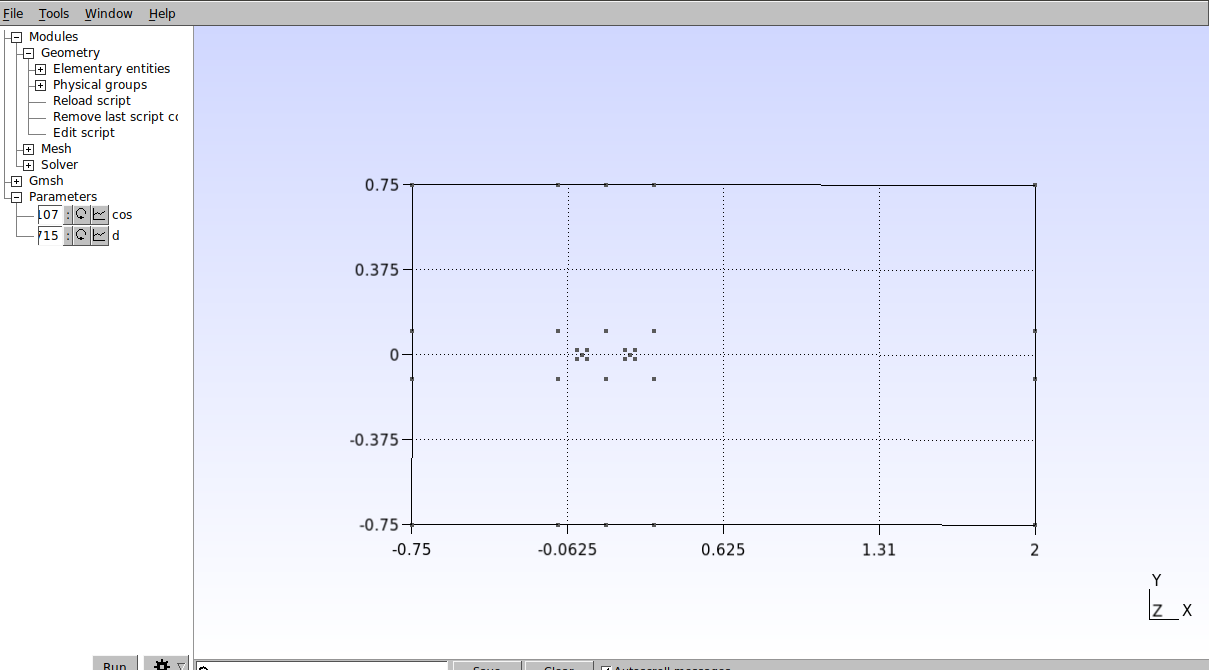
Vamos então gerar os arcos que definem os cilindros. Na interface gráfica, clique em Modules→Geometry→Elementary entities→Add →Circle arc. Em seguida selecione um ponto externo, depois o ponto central e então o outro ponto externo, conforme a figura abaixo.
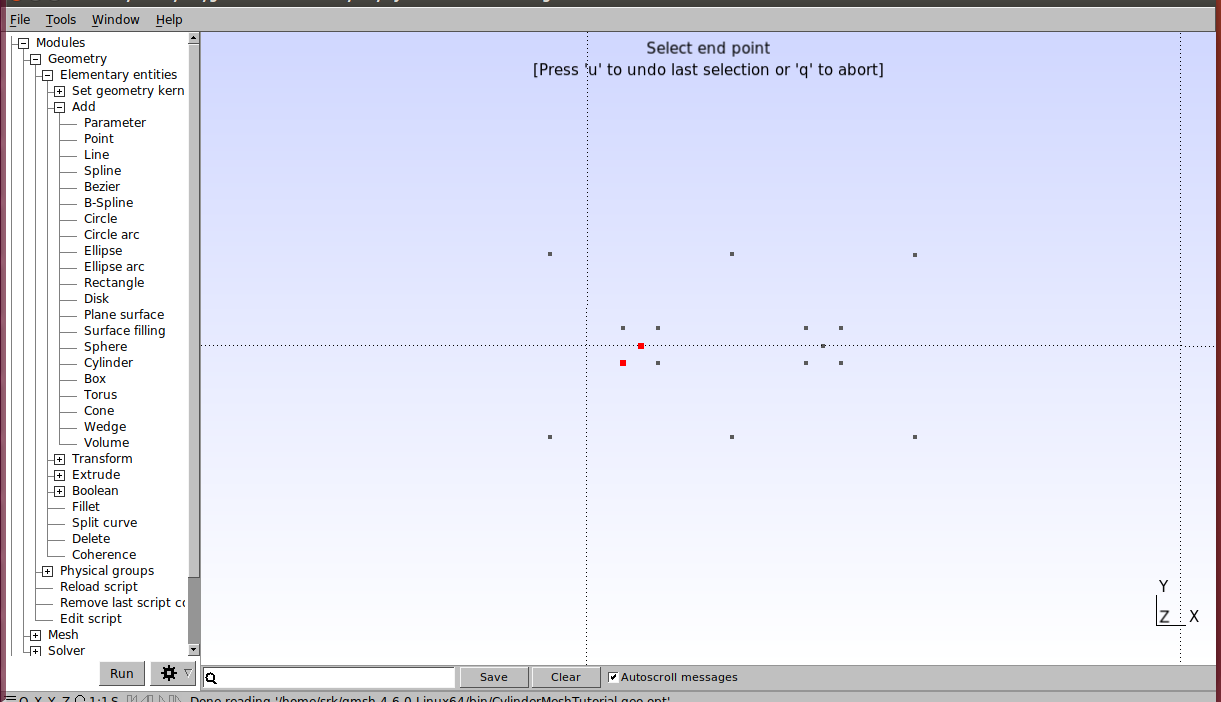
Repita esse procedimento para construir o círculo dos dois cilindros. O resultado é o seguinte.
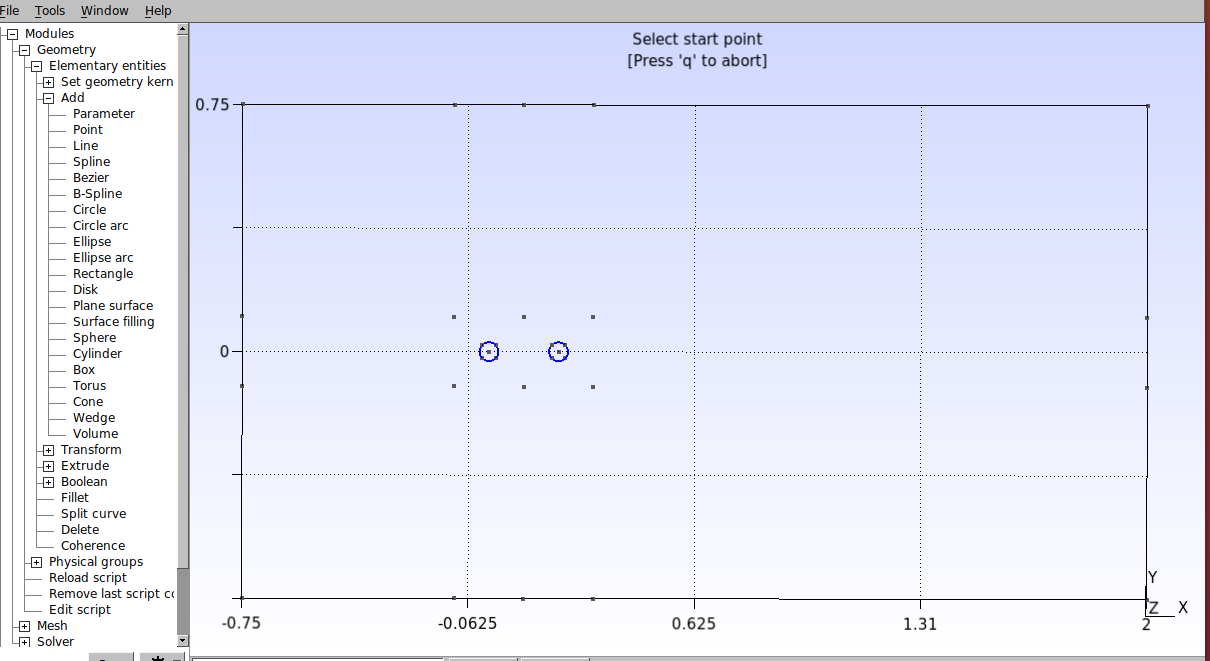
Para definir as linhas do domínio é importante manter uma convenção, isso porque a ordem em que os pontos são interligados vai determinar a direção do crescimento dos elementos no momento em que refinarmos a malha. Primeiramente vá até Modules→Geometry→Elementary entities→Add →Line. Interligue os pontos sempre da parte mais interna do domínio para a parte mais externa, conforme indicado pelas flechas na figura a seguir.
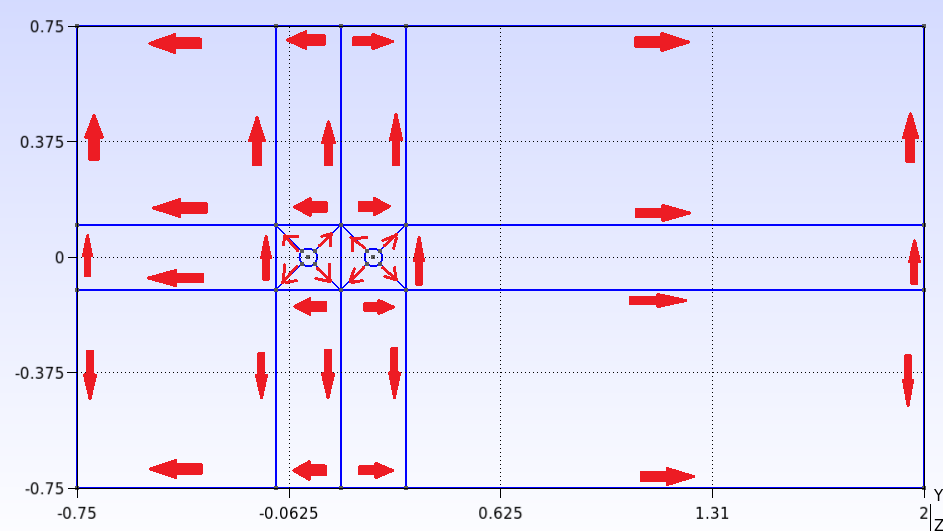
No script, essas mudanças são feitas com os seguintes comandos:
// Linhas e arcos que definem o domínio
Circle(1) = {5, 1, 4};
Circle(2) = {4, 1, 3};
Circle(3) = {3, 1, 6};
Circle(4) = {6, 1, 5};
Circle(5) = {9, 2, 8};
Circle(6) = {8, 2, 7};
Circle(7) = {7, 2, 10};
Circle(8) = {10, 2, 9};
Line(9) = {27, 11};
Line(10) = {17, 21};
Line(11) = {18, 22};
Line(12) = {28, 12};
Line(13) = {19, 23};
Line(14) = {29, 13};
Line(15) = {30, 14};
Line(16) = {18, 28};
Line(17) = {16, 26};
Line(18) = {20, 30};
Line(19) = {19, 29};
Line(20) = {15, 25};
Line(21) = {17, 27};
Line(22) = {20, 24};
Line(23) = {21, 11};
Line(24) = {22, 12};
Line(25) = {22, 21};
Line(26) = {18, 17};
Line(27) = {16, 15};
Line(28) = {20, 19};
Line(29) = {17, 15};
Line(30) = {18, 16};
Line(31) = {16, 20};
Line(32) = {15, 19};
Line(33) = {27, 25};
Line(34) = {25, 29};
Line(35) = {23, 13};
Line(36) = {24, 14};
Line(37) = {24, 23};
Line(38) = {28, 26};
Line(39) = {26, 30};
Line(40) = {4, 17};
Line(41) = {3, 15};
Line(42) = {5, 18};
Line(43) = {6, 16};
Line(44) = {9, 16};
Line(45) = {10, 20};
Line(46) = {7, 19};
Line(47) = {8, 15};
A próxima etapa é definir as superfícies. Clique em Modules→Geometry→Elementary entities→Add →Plane Surface e selecione as quatro linhas que definem cada superfície, como mostrado abaixo. Aperte, então, a tecla “e” para confirmar a seleção e, assim, devem aparecer linhas tracejadas dentro da superfície.

Repita esse procedimento para todas as superfícies. O resultado deve ser o seguinte:
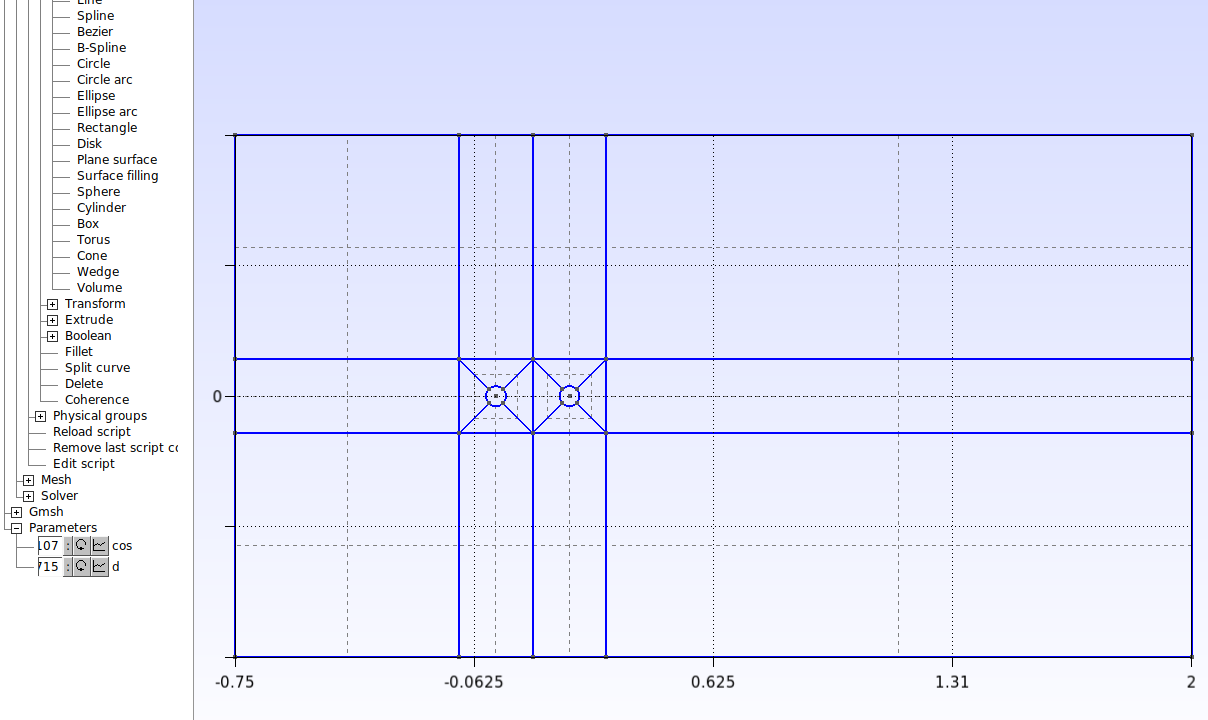
Agora vamos recombinar as superfícies para obter uma malha estruturada. Clique em Modules→Mesh→Define→Recombine. Selecione então todas as superfícies, como mostrado abaixo, e depois pressione a tecla “e” para confirmar.
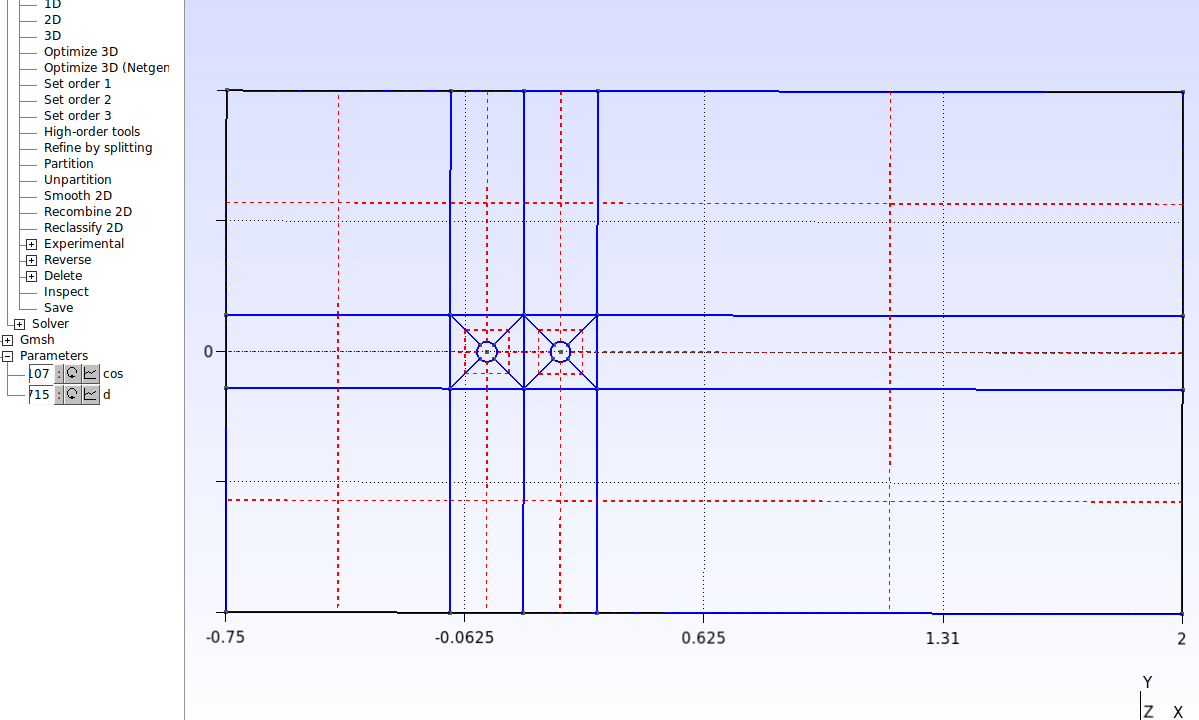
No script, esses procedimentos são feitos com os comandos abaixo:
// Definição das superfícies
Curve Loop(1) = {21, 9, -23, -10};
Plane Surface(1) = {1};
Curve Loop(2) = {21, 33, -20, -29};
Plane Surface(2) = {2};
Curve Loop(3) = {20, 34, -19, -32};
Plane Surface(3) = {3};
Curve Loop(4) = {19, 14, -35, -13};
Plane Surface(4) = {4};
Curve Loop(5) = {13, -37, -22, 28};
Plane Surface(5) = {5};
Curve Loop(6) = {22, 36, -15, -18};
Plane Surface(6) = {6};
Curve Loop(7) = {18, -39, -17, 31};
Plane Surface(7) = {7};
Curve Loop(8) = {17, -38, -16, 30};
Plane Surface(8) = {8};
Curve Loop(9) = {16, 12, -24, -11};
Plane Surface(9) = {9};
Curve Loop(10) = {11, 25, -10, -26};
Plane Surface(10) = {10};
Curve Loop(11) = {26, -40, -1, 42};
Plane Surface(11) = {11};
Curve Loop(12) = {4, 42, 30, -43};
Plane Surface(12) = {12};
Curve Loop(13) = {43, 27, -41, 3};
Plane Surface(13) = {13};
Curve Loop(14) = {2, 41, -29, -40};
Plane Surface(14) = {14};
Curve Loop(15) = {27, -47, -5, 44};
Plane Surface(15) = {15};
Curve Loop(16) = {44, 31, -45, 8};
Plane Surface(16) = {16};
Curve Loop(17) = {45, 28, -46, 7};
Plane Surface(17) = {17};
Curve Loop(18) = {46, -32, -47, 6};
Plane Surface(18) = {18};
Recombine Surface {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 14, 13, 12, 15, 18, 17, 16};
Para definir as taxas de crescimento dos elementos, vamos utilizar a função “Transfinite”. Clique em Modules→Mesh→Define→Transfinite→Curve. Digite o número de pontos e o parâmetro de crescimento que aparecem na janela “Mesh context” e depois selecione as linhas conforme mostrado na figura abaixo. Feito isso, aperte a tecla “e” para confirmar.
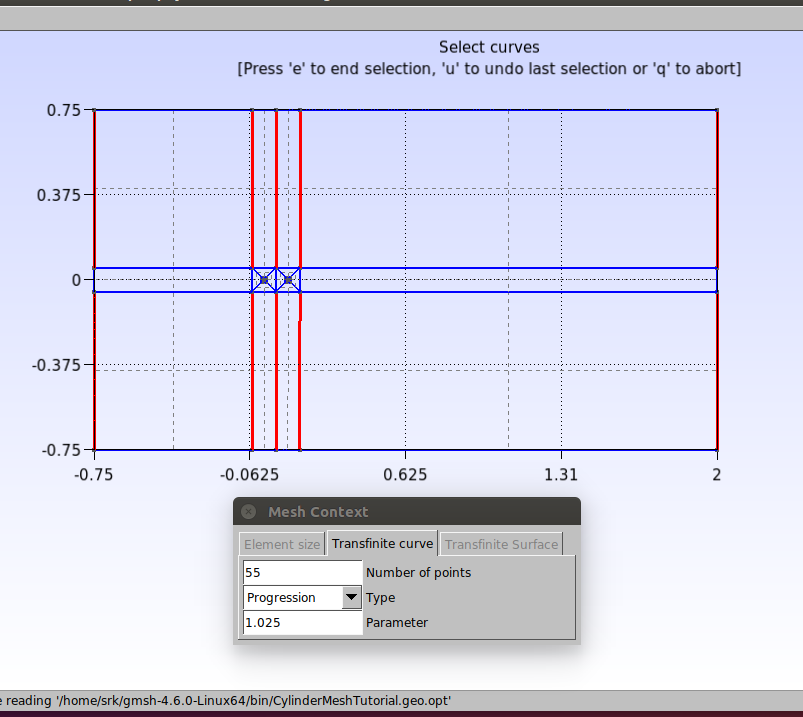
Repita esse procedimento para todas as curvas restantes, conforme indicado pelas figuras abaixo.
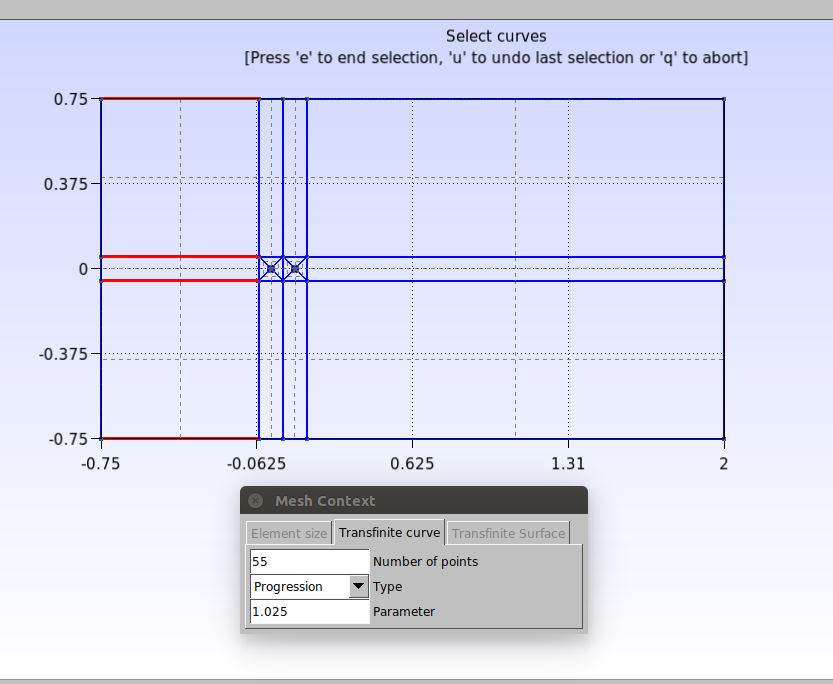
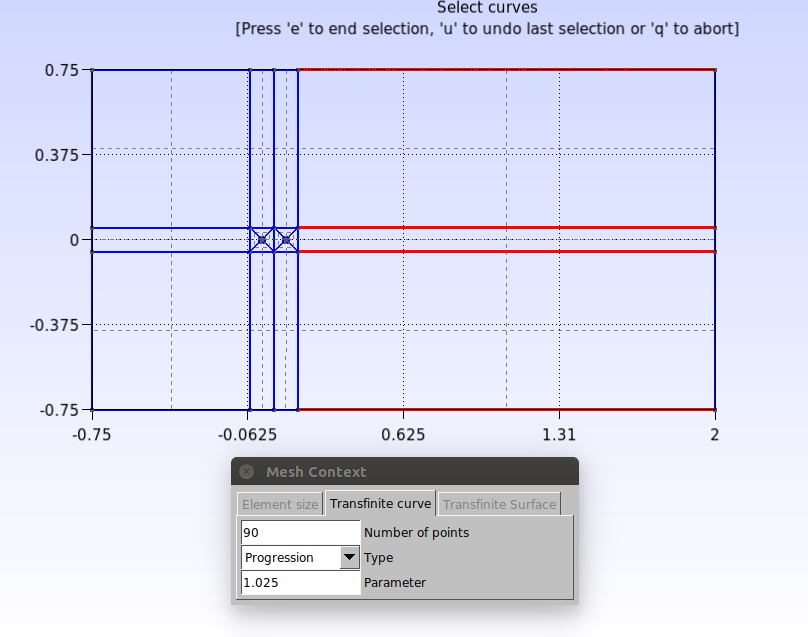
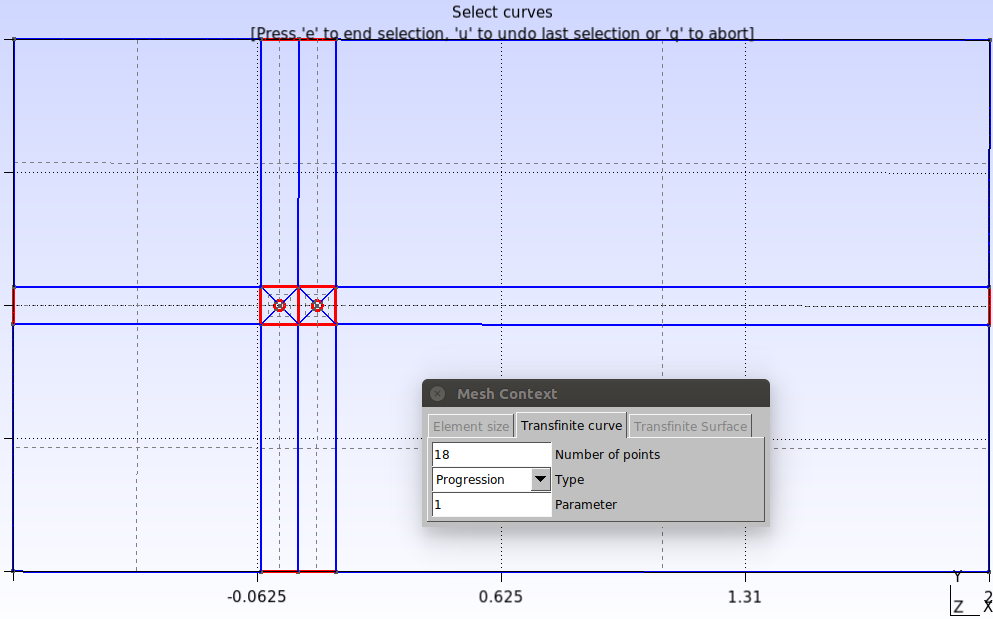
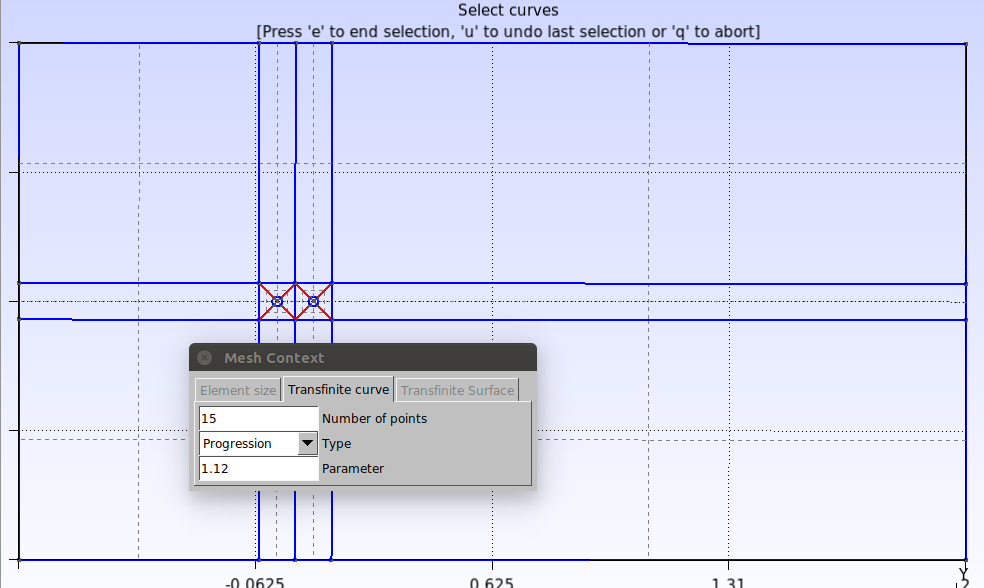
No script isso é feito da seguinte maneira:
Transfinite Curve {23, 21, 20, 19, 35, 24, 16, 17, 18, 36} = 55 Using Progression 1.025;
Transfinite Curve {9, 10, 11, 12} = 55 Using Progression 1.025;
Transfinite Curve {14, 13, 22, 15} = 90 Using Progression 1.025;
Transfinite Curve {1, 26, 25, 2, 29, 33, 4, 30, 38, 8, 31, 39, 6, 32, 34, 7, 28, 37, 3, 27, 5} = 18 Using Progression 1;
Transfinite Curve {40, 42, 43, 41, 47, 44, 45, 46} = 15 Using Progression 1.12;
Agora vamos aplicar a função “Transfinite” em cada superfície. Clique em Modules→Mesh→Define→Transfinite→Surface e selecione a superfície clicando nas linhas tracejadas que estão em seu interior, como indicado na figura abaixo, e aperte “e” para confirmar.
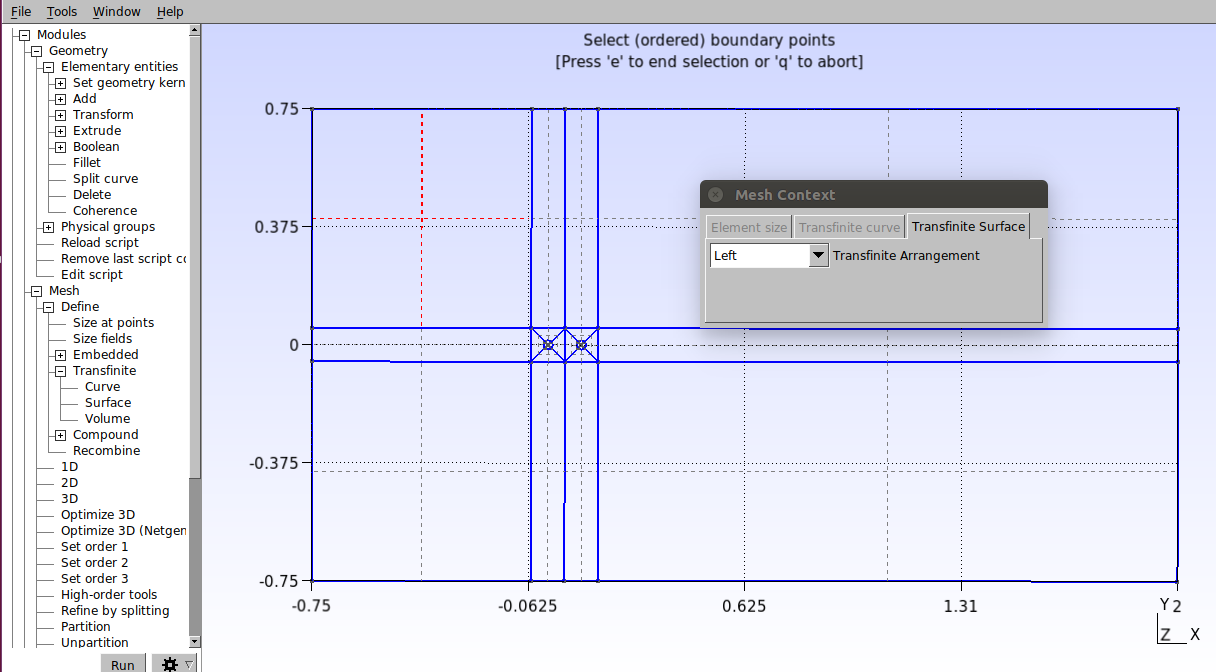
Repita esse procedimento para todas as superfícies. O script deve ter os seguintes comandos:
Transfinite Surface {1};
Transfinite Surface {2};
Transfinite Surface {3};
Transfinite Surface {4};
Transfinite Surface {5};
Transfinite Surface {6};
Transfinite Surface {7};
Transfinite Surface {8};
Transfinite Surface {9};
Transfinite Surface {10};
Transfinite Surface {11};
Transfinite Surface {14};
Transfinite Surface {13};
Transfinite Surface {12};
Transfinite Surface {15};
Transfinite Surface {18};
Transfinite Surface {17};
Transfinite Surface {16};
O próximo passo é extrudar a malha. Clique em Modules→Geometry→Elementary entities→Add→Extrude→Translate. Na janela que abrir, configure os valores de acordo com o indicado na figura abaixo e marque a opção “Extrude mesh”. Em seguida selecione todas as superfícies e aperte “e” para confirmar.
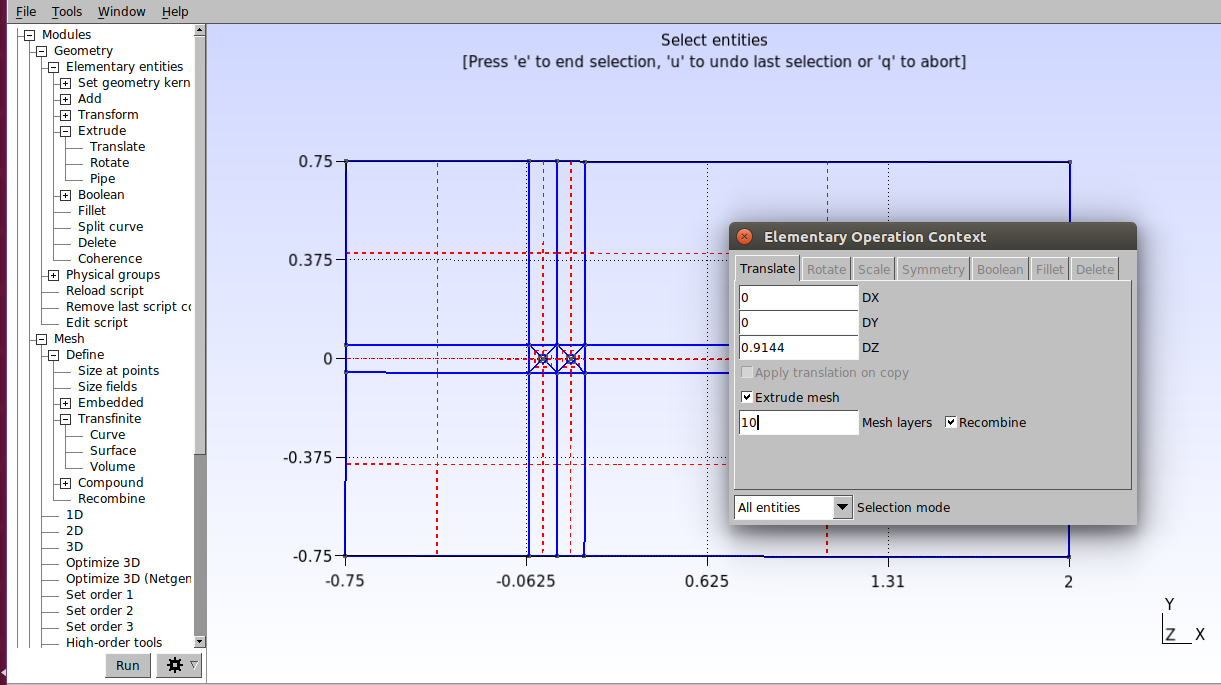
No script devem ser inseridos os seguintes comandos:
Extrude {0, 0, 0.9144} {
Surface{1}; Surface{2}; Surface{3}; Surface{4}; Surface{10}; Surface{11}; Surface{14}; Surface{12}; Surface{13}; Surface{15}; Surface{18}; Surface{17}; Surface{16}; Surface{5}; Surface{6}; Surface{7}; Surface{8}; Surface{9}; Layers{10}; Recombine;
}
Por fim, vamos definir as faces que serão responsáveis pelas condições de contorno na simulação. Clique em Modules→Geometry→Physical groups→Add→Surface. Na janela que abrir digite o nome “inlet”, selecione as três superfícies da entrada como indicado na imagem abaixo e então aperte a tecla “e” para confirmar.
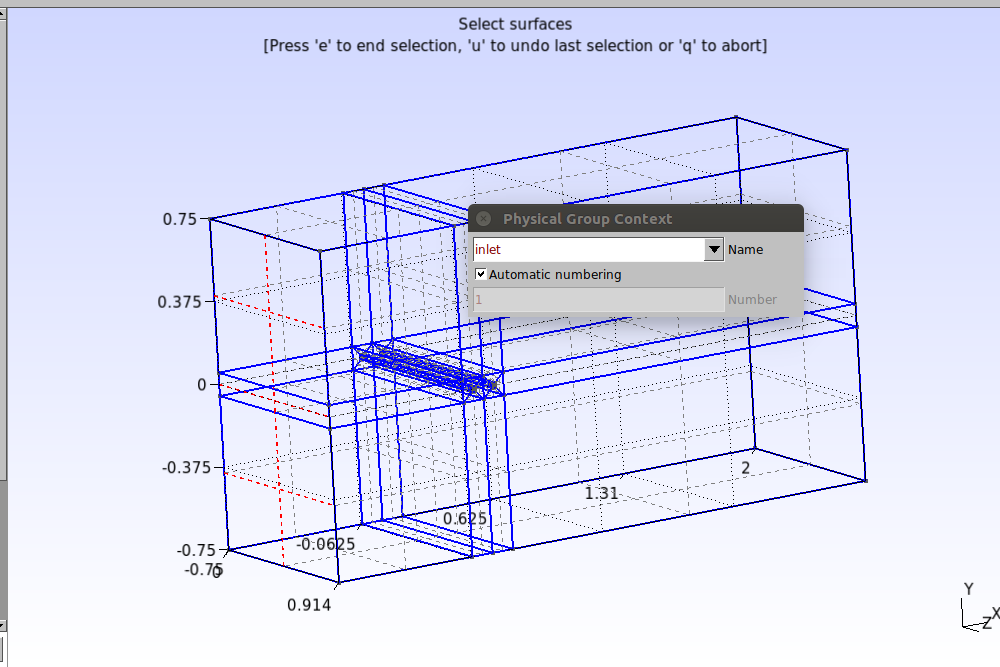
Repita o procedimento para os demais grupos, como indicam as imagens abaixo
Saída:
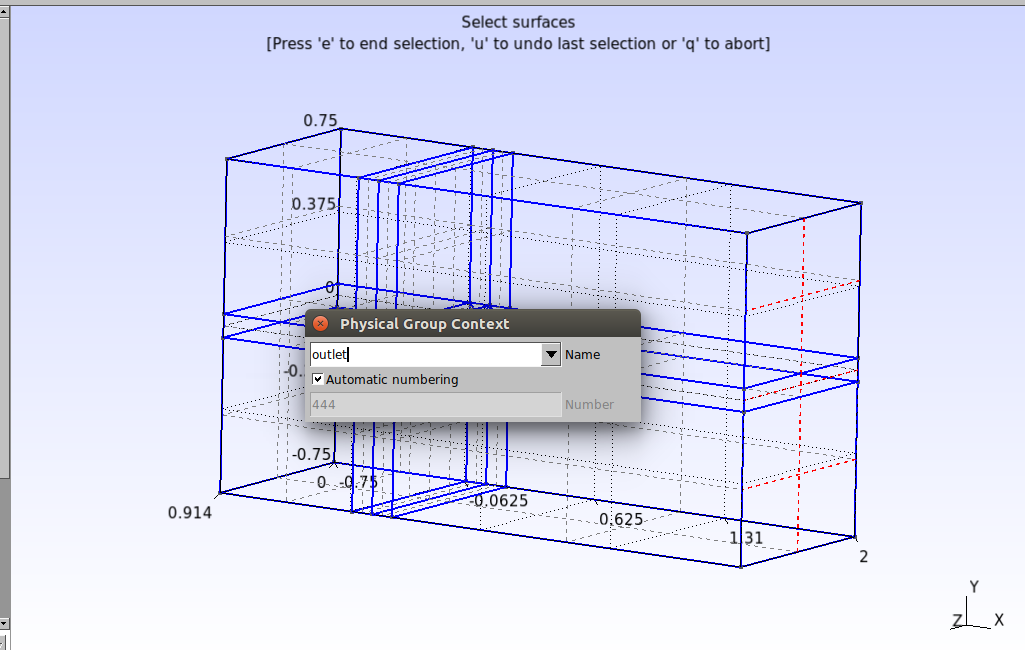
Partes da frente e atrás:
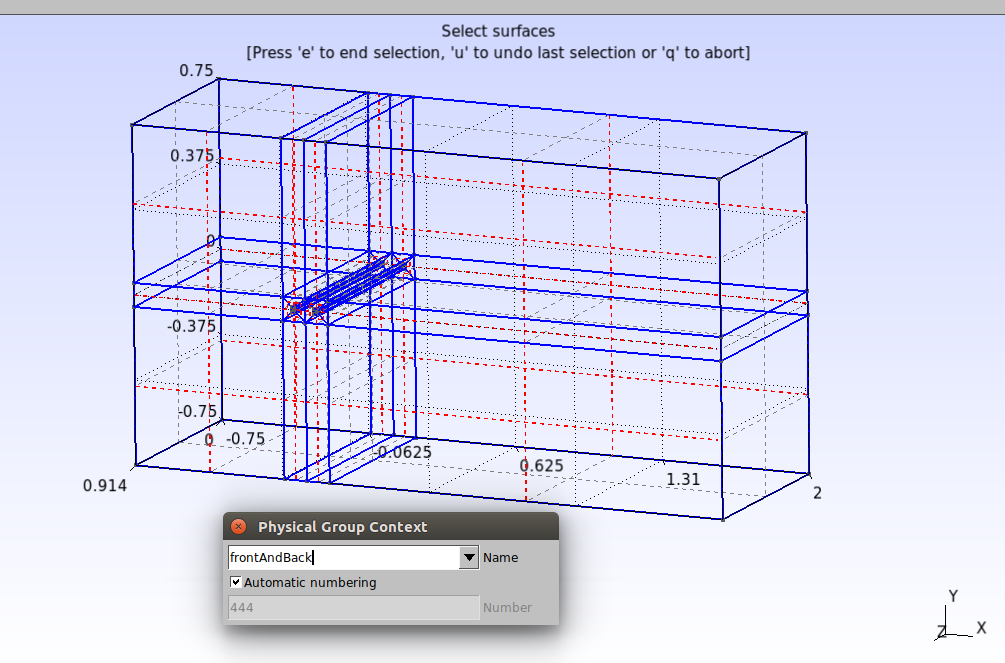
Partes de baixo e de cima:
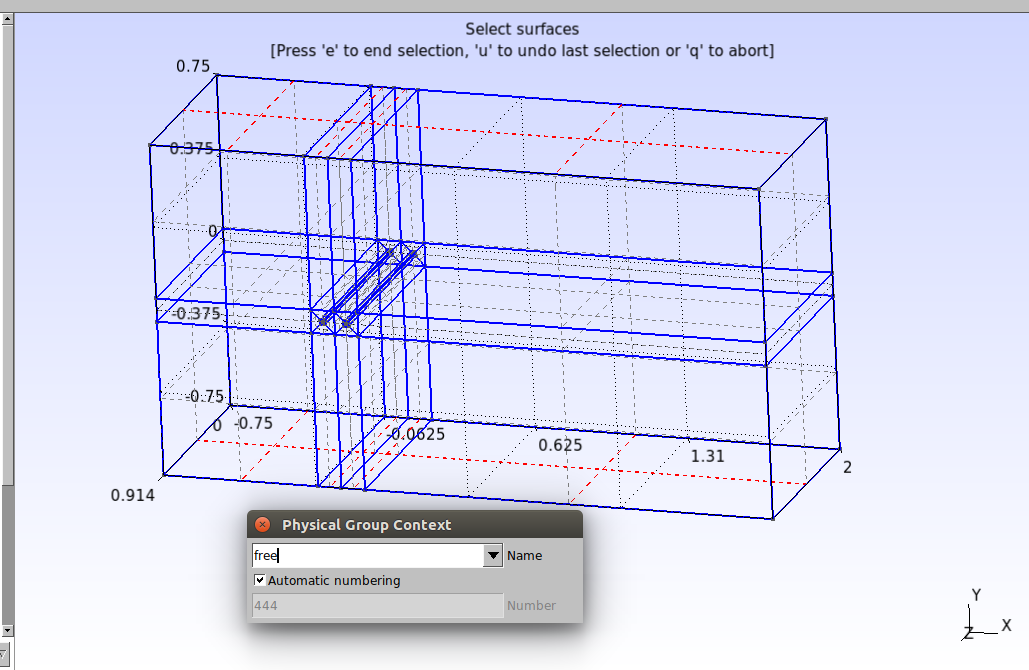
As quatro superfícies do cilindro 1:
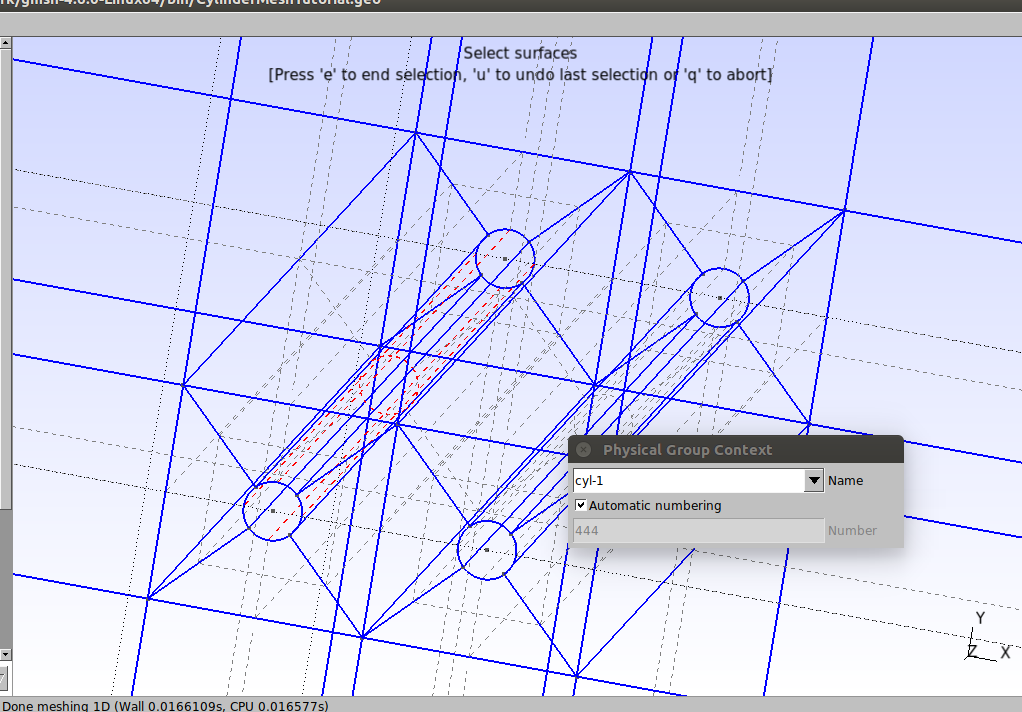
As quatro superfícies do cilindro 2:
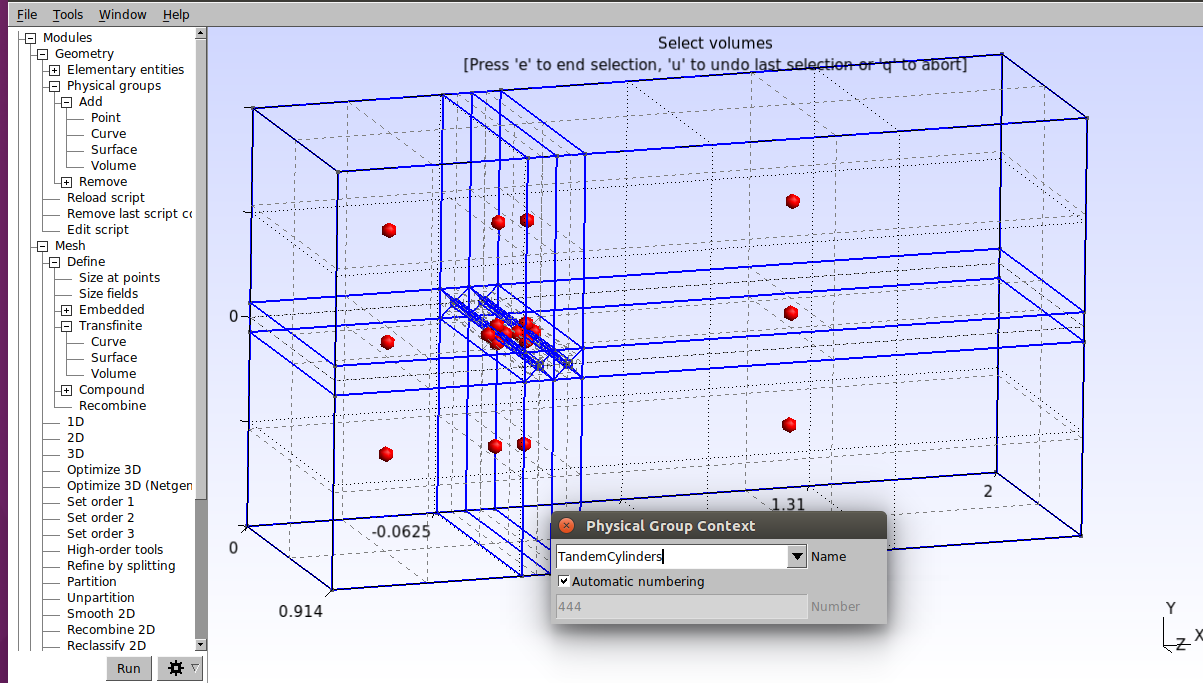
Agora clique em Modules→Geometry→Physical groups→Add→Volume e na janela que abrir digite “TandemCylinders” como nome e então selecione todas as esferas conforme mostrado abaixo. Aperta a tecla “e” para confirmar.
No script, isso é feito pelos seguintes comandos:
Physical Surface("inlet") = {64, 148, 438};
Physical Surface("outlet") = {130, 346, 368};
Physical Surface("frontAndBack") = {69, 91, 113, 135, 355, 377, 399, 421, 443, 157, 179, 201, 245, 223, 267, 289, 311, 333, 4, 5, 6, 7, 8, 9, 10, 1, 2, 3, 15, 18, 17, 16, 13, 14, 11, 12};
Physical Surface("free") = {126, 104, 82, 60, 372, 390, 412, 434};
Physical Surface("cyl-1") = {210, 174, 188, 244};
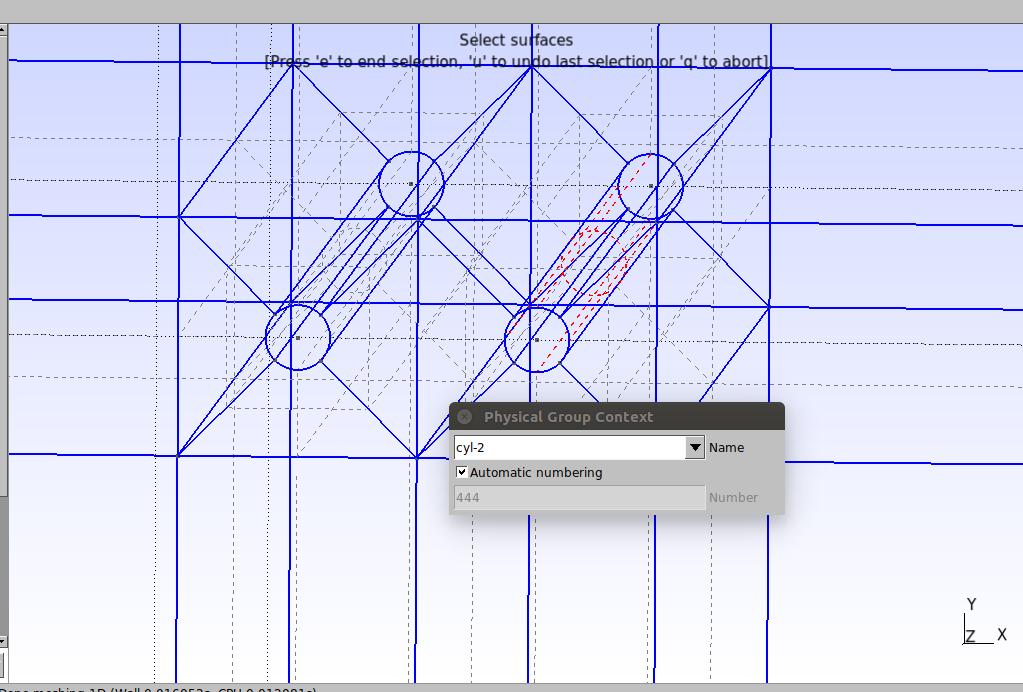
Physical Surface("cyl-2") = {262, 332, 310, 288};
Physical Volume("TandemCylinders") = {1, 2, 3, 4, 5, 6, 7, 9, 8, 10, 11, 12, 13, 14, 15, 16, 17, 18};
As configurações da malha já estão prontas. Para gerá-la clique em Modules→Mesh→3D. O resultado deve ser o seguinte:

Obs: caso não sejam mostrados os elementos da malha ao fazer o procedimento acima, clique duas vezes no eixo de coordenadas na parte de baixo à direita, como mostrado acima, e clique em “Mesh visibility” e marque a opção “2D element edges”.
Para exportar a malha vá até a barra de cima no Gmsh em File→Export e salve-a com o nome “TandemCylinders.msh”. Na janela que abrir escolha o formato “Version 2 ASCII” como mostrado abaixo e clique em “Ok”.
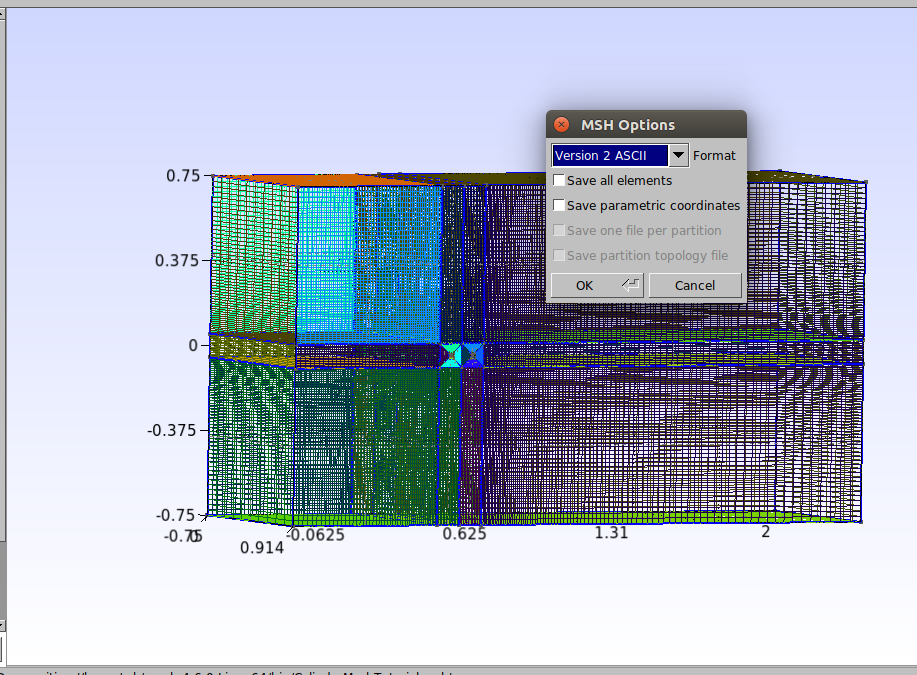
Pronto, o arquivo “TandemCylinders.msh” já pode ser importado no OpenFOAM.
Geração das superfícies utilizadas na analogia acústica
Para realizar a simulação do caso (ver tutorial), juntamente com analogias acústicas, é necessário gerar superfícies que englobem as fontes de ruído. Vamos gerar essas superfícies no Gmsh.
Primeiro, crie um novo arquivo clicando em File→New. Vamos criar os pontos da superfície. Clique em Modules→Geometry→Edit script e insira os seguintes pontos:
Point(1) = {-0.085, 0.16, 0, 1.0};
Point(2) = {-0.085, -0.16, 0, 1.0};
Point(3) = {0.57, 0.16, 0, 1.0};
Point(4) = {0.57, -0.16, 0, 1.0};
Salve o script e depois, no Gmsh, clique em Modules→Geometry→Reload script.
Vamos unir os pontos para formar um retângulo. Clique em Modules→Geometry→Elementary entities→Add→Line. Clique sobre dois pontos para gerar uma reta (Como nesse caso não vamos utilizar taxa de crescimento, os pontos podem ser ligados em qualquer ordem). Ao final você deve obter o seguinte resultado:
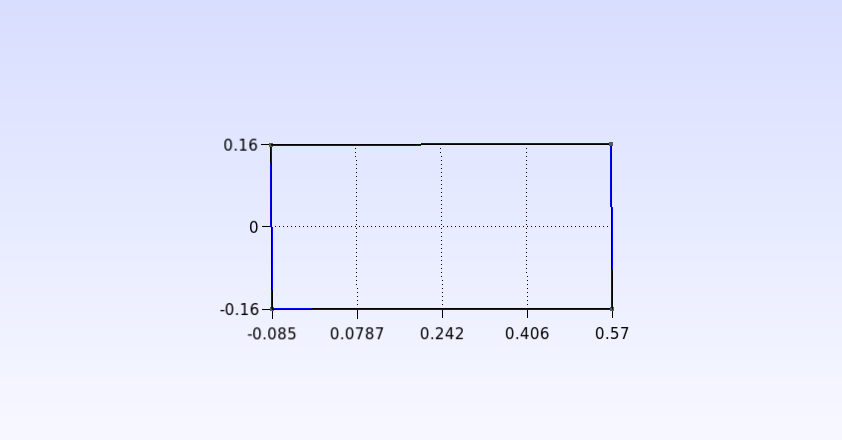
Para criar a superfície clique em Modules→Geometry→Elementary entities→Add→Plane Surface. Selecione todas as retas que formam o retângulo, como mostrado abaixo, e aperte “e” para confirmar.
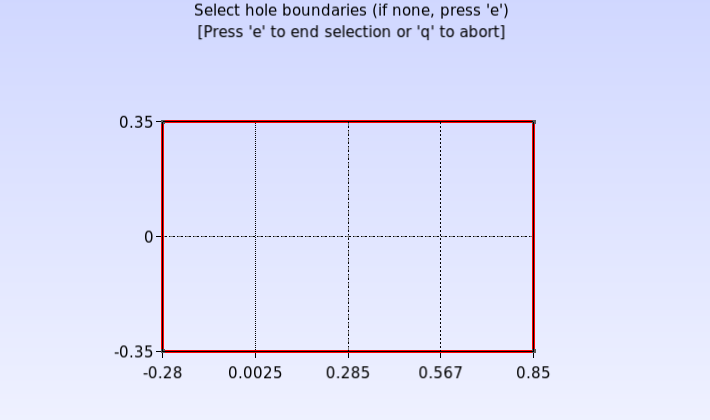
Agora aplique a função “Recombine” clicando em Modules→Mesh→Define→Recombine. Selecione a superfície clicando nas linhas tracejadas e aperte “e” para confirmar.

Vamos aplicar a função “Transfinite” para fazer o refino da malha. Clique em Modules→Mesh→Define→Transfinite→Curve. Na janela que abrir defina o número de pontos como 70, selecione as retas horizontais e aperte “e” para confirmar.
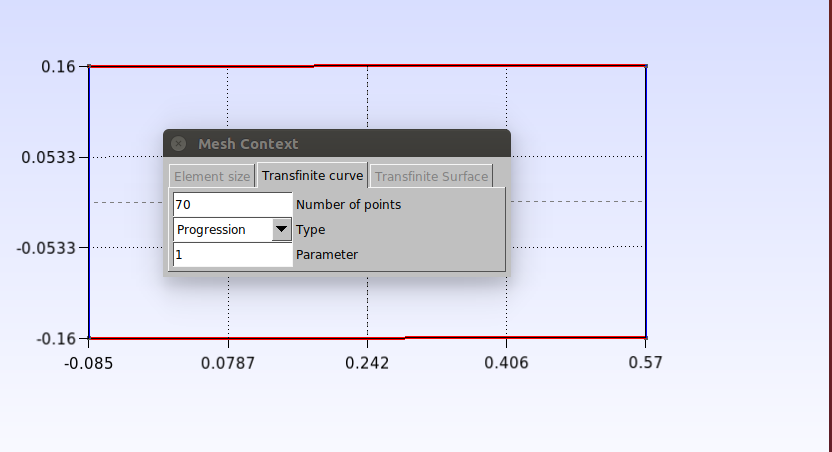
Depois, com a janela ainda aberta, altere o número de pontos para 40, selecione as retas verticais e aperte “e” para confirmar.

Clique, agora, em Modules→Mesh→Define→Transfinite→Surface, selecione a superfície clicando nas linhas tracejadas e aperte “e” para confirmar.
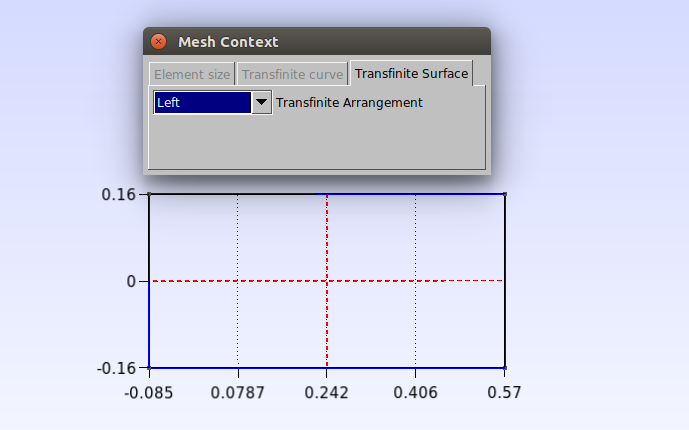
O próximo passo é extrudar a superfície. Clique em Modules→Geometry→Elementary entities→Extrude→ Translate. Na janela que abrir configure os valores como mostrado abaixo, selecione a superfície clicando nas linhas tracejadas no interior da superfície e aperte “e” para confirmar.
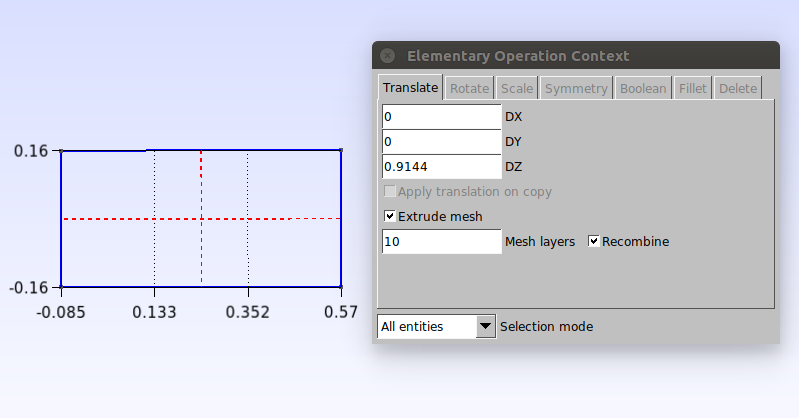
O script final da superfície fica da seguinte forma:
Point(1) = {-0.085, 0.16, 0, 1.0};
Point(2) = {-0.085, -0.16, 0, 1.0};
Point(3) = {0.57, 0.16, 0, 1.0};
Point(4) = {0.57, -0.16, 0, 1.0};
Line(1) = {1, 3};
Line(2) = {3, 4};
Line(3) = {4, 2};
Line(4) = {2, 1};
Curve Loop(1) = {1, 2, 3, 4};
Plane Surface(1) = {1};
Recombine Surface {1};
Transfinite Curve {1, 3} = 70 Using Progression 1;
Transfinite Curve {4, 2} = 40 Using Progression 1;
Transfinite Surface {1};
Extrude {0, 0, 0.9144} {
Surface{1}; Layers{10}; Recombine;
}
Para criar a malha da superfície tridimensional clique em Modules→Mesh→3D. Já para exportá-la vá até File→Export. Coloque o nome do arquivo como “superficie1.stl”, escolha o local onde ela será salva e clique em “Save”. Na janela “STL Options” que abrir certifique de selecionar as opções como mostradas abaixo.
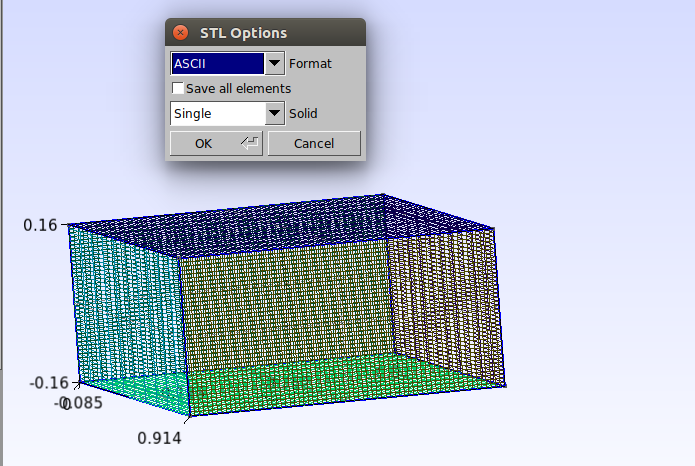
A segunda superfície a ser utilizada é semelhante a primeira. A partir do script da primeira, altere a posição dos pontos e também o número de pontos utilizados na função “Transfinite” conforme mostrado abaixo.
Point(1) = {-0.28, 0.35, 0, 1.0};
Point(2) = {-0.28, -0.35, 0, 1.0};
Point(3) = {0.85, 0.35, 0, 1.0};
Point(4) = {0.85, -0.35, 0, 1.0};
Line(1) = {1, 3};
Line(2) = {3, 4};
Line(3) = {4, 2};
Line(4) = {2, 1};
Curve Loop(1) = {1, 2, 3, 4};
Plane Surface(1) = {1};
Recombine Surface {1};
Transfinite Curve {1, 3} = 90 Using Progression 1;
Transfinite Curve {4, 2} = 55 Using Progression 1;
Transfinite Surface {1};
Extrude {0, 0, 0.9144} {
Surface{1}; Layers{10}; Recombine;
}
Recarregue o script e para finalizar, repita o processo de criação da malha 3D e de sua exportação como descrito para a superfície 1. Salve-a com o nome “superficie2.stl”.