Modelos de ordem reduzida em eng. Aeroespacial

Heidmann – Método

Contextualização
- Ruído e motor aeronáutico

Explicação do Modelo de Heidmann
Referências

Modelo semi-empírico de previsão de ruído em motores aeronáuticos

Contextualização

Segundo Smith (1989), muitas das inovações tecnológicas da humanidade vieram acompanhadas de efeitos colaterais, efeitos que por sua vez indesejados. Tem-se como exemplo o advento da locomotiva, o qual foi excelente para para a logística mundial, porém com ela também existiram as cortinas de fumaça deixadas sobre os trilhos e seus ruidosos vagões. Não é diferente quando o assunto é ruído aeronáutico, este que por sua vez, tornou o mundo mais rápido, encurtou o tempo de viagens, e ao mesmo tempo o tornou mais barulhento com seus motores.

Na figura abaixo, é possível ver as principais fontes de ruído em um avião.

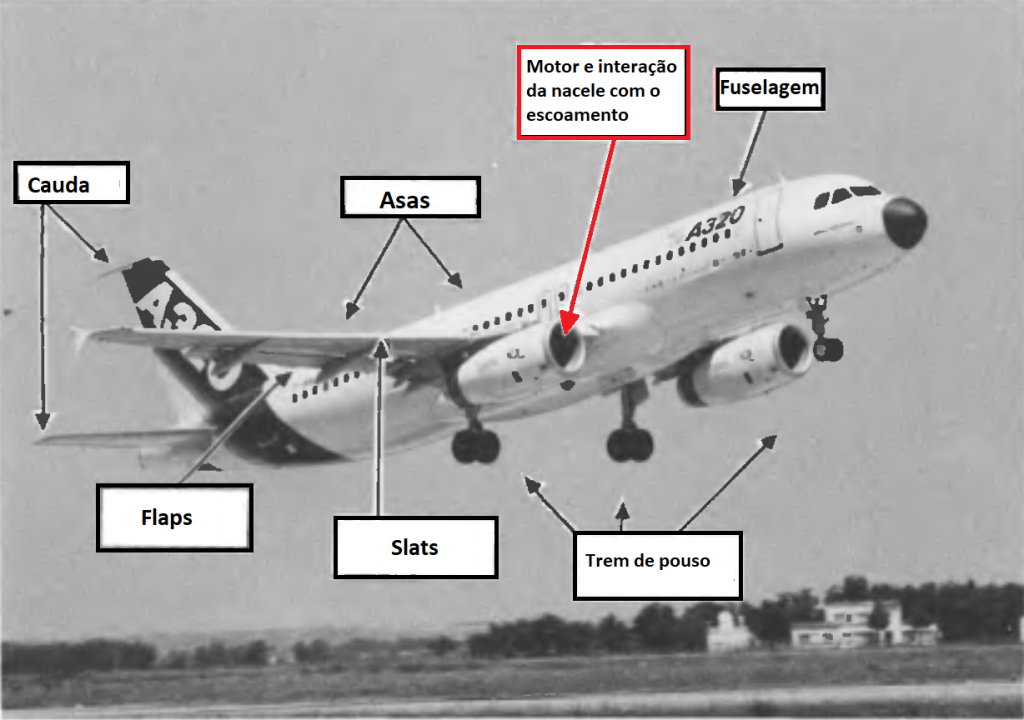
Figura 1 – Principais fontes de ruído num avião (SMITH, 1989)

Com uso crescente dos motores turbojatos a partir da década de 60, os quais extremamente ruidosos foi surgindo a necessidade de motores silenciosos, fazendo com que estudos na área de ruídos fosse aprimorada.

Ruído e motor aeronáutico

Um esquemático do motor pode ser visto abaixo, é possível ver o duto de entrada (A), duto de saída (B) e o ângulo de diretividade da localização de um receptor até o eixo axial do duto de entrada.

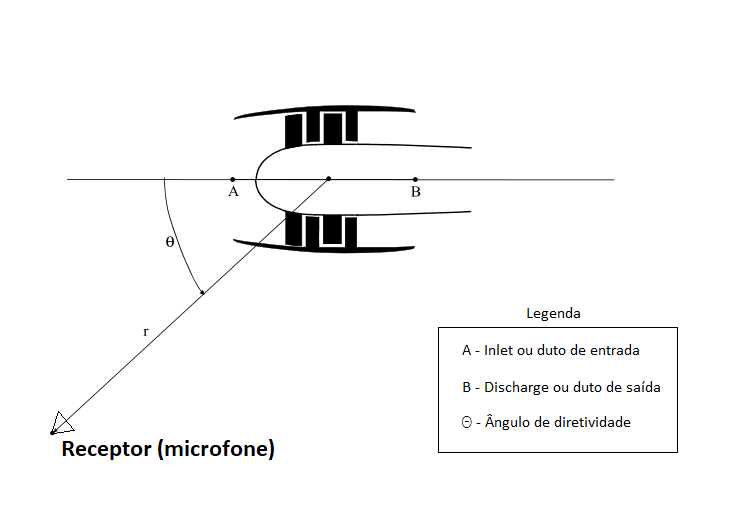
Figura 2 – Descrição de alguns parâmetros a serem utilizados para o método de Heidmann, ESDU (2003)

O ruído no motor pode ser divido em três partes: o jato, a interação do jato com as superfícies da aeronave e o ruído do próprio motor.

O espectro da frequência do ruído é constituído por um uma faixa em broadband , discrete tones e combination tones.

Broadband (banda larga)

O ruido de banda larga é um ruido baseado em uma ampla faixa de frequências, segundo Smith (1989), a componente de broadband é criada a partir das flutuações na pressão e associado com um escoamento turbulento nas camadas limites das pás tando do fan quanto as lâminas do compressor.

Discrete Tones (tonais)

Os tonais são causados pelo movimento cíclico das pás em relação a um observador parado, para SMITH (1989), sejam elas do fan, do compressor ou da própria turbina, pode-se observar ainda que os tonais possuem harmônicos que podem ser vistos na figura 3. A frequência desses tons discretos é, respectivamente, a própria frequência de rotação das pás (Blade Passing Frequency – BPF) e seus harmônicos.

Combination Tones

Os combination tones ocorrem devido ao fato de haver choque na ponta das pás do fan, são referentes ao ruído conhecido como buzzsaw noise, tal ruído leva o nome devido a semelhança de som uma motosserra e não a “combinação” a qual o nome pode levar a confusão.

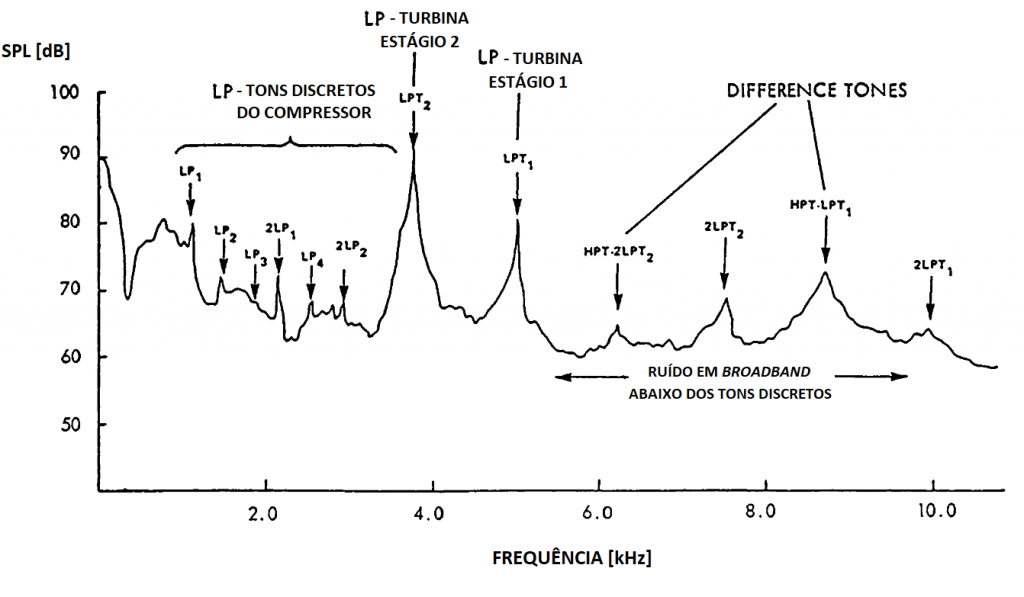
Figura 3 – Caracterização do espectro de ruído para um motor aeronáutico (SMITH, 1989)

Explicação do método de Heidmann

O método foi desenvolvido por Marcus F. Heidmann, NASA Lewis Research Center, e pode ser encontrado em NASA X-71763. A explicação a ser dada é um resumo, caso o usuário queira uma explcação completa com exemplo de aplicação das funções, isso pode ser feito clicando aqui. O modelo de Heidmann (1979) surge justamente para melhorar o método de predição já existente fruto da colaboração entre Boeing e AMES (NASA), tal evolução propõe, além de poder compreender outros motores, reportar e especificar um método interino para fan e compressor como fonte de ruído nos termos de espectro de campo livre e diretividade.

A predição consiste em um conjunto de componentes calculados separadamente e depois relacionados em NPS, onde nível de ruído predito é contabilizado em bandas com um-terço de oitava, essas componentes podem ser vistas abaixo:

Ruído do fan ou compressor emitido pelo duto de entrada da nacele (inlet) :
- broadband ;
- discrete tones;
- combination tone.
Ruído emitido pelo duto de saída (discharge-duct):
- broadband ;
- discrete tones.

O resumo do passo a passo segundo Heidmann pode ser simplificado na figura 4, e logo abaixo a explicação da mesma figura.

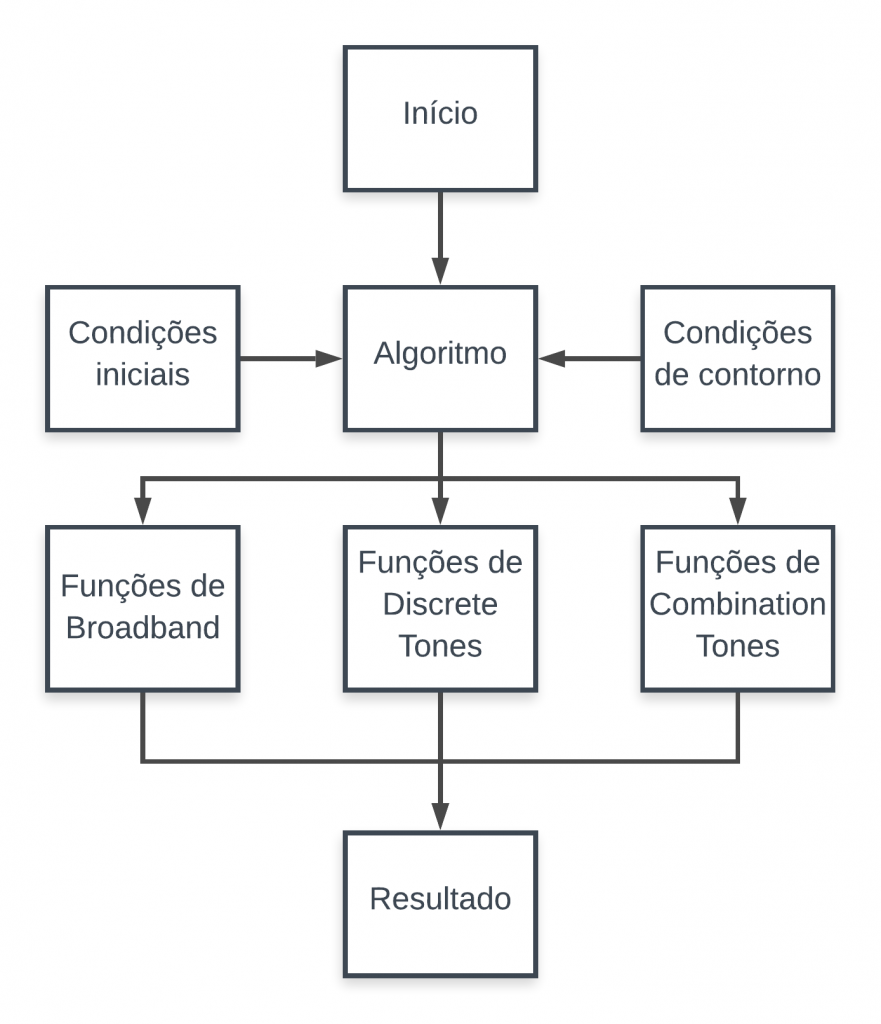
Figura 4 – Resumo do método de Heidmann em esquema de fluxograma, Autor.

Caracteristicas geométricas

As características geométricas do motor são:

Número de lâminas no rotor e estator;
Tipo de motor: pequeno ou grande;
Se o motor possui Inlet Guide Vanes;
Quantos estágios de fan o motor possui;

Condições operacionais e configuração do método

Posições dos receptores em relação ao motor;
Tipo de interpolação a ser usada.
Números de Mach na ponta de pá;
Número de Mach no ponto de design da pá;
Frequência de passagem da pá do fan (BPF).

Funções de Broadband

As funções retornam uma matriz com os dados da faixa que representam a banda larga, $Lc$ é o nível se pressão sonora característico e $SPL$ é o nível de pressão sonora em função da frequência.

$\displaystyle Lc = 20\log_{10}\frac{\Delta T}{ \Delta T_o } + 10\log_{10} \frac{m}{m_o} + F_1\left [ \left ( M_{TR} \right ), \left ( M_{TR_D} \right ) \right ] + F_2(RSS) + F_3(\theta)$

$\displaystyle SPL = Lc+ F_4(\frac{f}{BPF})$

Funções de Discrete tones

No caso dos Tons Discretos os dados de saída apresentam informações dos “picos” referentes a componente de rotação das pás do fan.

$\displaystyle Lc = 20\log_{10}\frac{\Delta T}{ \Delta T_o } + 10\log_{10} \frac{m}{m_o} + F_1\left [ \left ( M_{TR} \right ), \left ( M_{TR_D} \right ) \right ] + F_2(RSS) + F_3(\theta) + C$

$\displaystyle SPL = Lc+ 10 \log_{10} ( 10^{0.1F_4(\frac{f}{BPF})} + 10^{0.1F_5(\frac{f}{BPF})} )$

Funções de Combination tones

A saída desta função, assim como os tons discretos, são os dados dos pontos onde ocorre o buzzsaw noise.

$\displaystyle Lc = 20\log_{10}\frac{\Delta T}{ \Delta T_o } + 10\log_{10} \frac{m}{m_o} + F_1\left ( M_{TR} \right ) + F_2(\theta) + C$

$\displaystyle SPL = Lc+ F_3(\frac{f}{BPF})$

Resultado

O resultado do algoritmo é uma matriz que representa a soma em pressão das funções SPL apresentada acima, cujos valores estão em decibéis, as linhas da matriz representam as frequências escolhidas e as colunas os ângulos de diretividade. Para mais informações referente ao método e as funções apresentadas, olhar a seção Heidmann – Modelo.

Referencias

HEIDMANN, MARCUS F. Interim Prediction Method for Fan and Compressor Source Noise. 1979. ed. Estados Unidos: NASA Technical Memorandum, 1979. 68 p. . NASA TM X-71763

SMITH, MICHAEL J. T. Aircraft Noise. 1989. ed. Reino Unido: CAMBRIDGE UNIVERSITY PRESS, 1989. v. 1, cap. 3, p. 41-118. ISBN 0 521 33186 2.