Base de dados e modelo de rede neural
Base de dados
A base de dados de performance de diferenetes hélices pode ser encontrada em APC (2023), para os propósitos desse trabalho, foi utilizado as seguintes normalizações dos dados de entrada tanto geométricos quanto operacionais, sendo eles: a rotação (rev/s), a velocidade de escoamento live (m/s), o diâmetro (m) e pitch (m) da hélice (representados pelos símbolos ,
,
,
).
Desse modo, na base de dados normalizada, é possível obsevar em cada linha esses 4 parâmatros de entrada apresentando os correspondentes carregamentos aerodinâmicos, que no caso são os coeficientes de tração e potência.
Rede neural
Método de utilização
- Instalação:
Para utilizar a rede neural já treinada, é necessário baixar os modelos individualmente para os coeficientes de tração e de carregamento (caso haja interesse na utilização dos códigos, entrar em contato com os professores responsáveis pela página).
from AeroModelsPytorch import AeroModel Ct_regression = AeroModel.LoadModel('Ct-Model.model') Cp_regression = AeroModel.LoadModel('Cp-Caso-15.val.model')
- Definição de dados de entrada:
É necessário definir os dados de entrada com base nos parâmetros operacionais e geométricos da hélice (no caso a velocidade de escoamento livre já está normalizada como razão de avanço), formando assim um vetor de 4 elementos que deve ser colocado em um vetor numpy através da função numpy.column_stack() da seguinte forma:
D = 0.3 # m rho = 1.225 # kg/m^3 f = 5000/60 # Hz ni = 1.5e-5 # viscosidade cinemática m^2/s c0 = 343.3 # m/s Re = ((f*2*np.pi)/ni)*((D/2)**2) # Reynolds M_t = ((f*2*np.pi)/c0)*((D/2)) # Mach tip Jd = 0.60 # Design advance ratio J_reg = np.array([0 , 0.24 , 0.4 ,0.6]) Re_reg = np.full(len(J_reg), Re) Mtip = np.full(len(J_reg), M_t) Jd = np.full(len(J_reg), Jd) var = np.column_stack((Re_reg, Mtip, Jd, J_reg))
- Estimativa dos coeficientes:
A estimativa é feita a partir através da função CoefEval(), que tem como parâmetro os dados de entrada já definidos, e finalmente, esse resultado é multiplicado pelo número de pás que a hélice possui, como mostrado a seguir (nesse caso, a hélice possui duas pás):
Ct = 2*Ct_regression.CoefEval(var) Cp = 2*Cp_regression.CoefEval(var)
Resultados:
Os resultados da aplicação da regressão utilizando as rede neurais já treinadas para o caso de uma hélice de diâmetro de 12 in, pitch de 12 in, em condições de 5000 rpm e diferentes velocidades de escoamento livre (diferentes razões de avanço) podem vistos nas figuras 1 e 2.
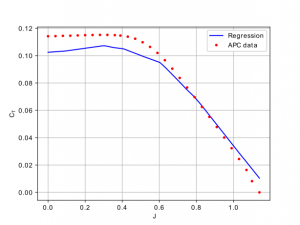
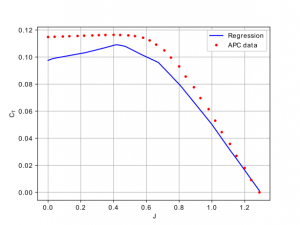
Figura 1: Regressão para o coeficiente de tração.
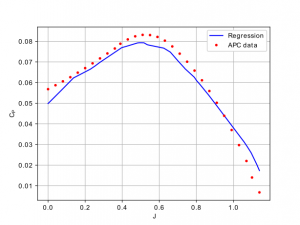
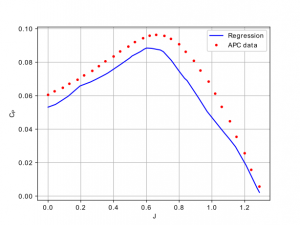
Figura 2: Regressão para o coeficiente de potência.
Referências
APC, 2023. “Apc propellers”. https://www.apcprop.com/technical-information/performance-data/ Accessed 15 Dez 2023.
de Carvalho, Pedro & Dutra da Silva, Filipe & Cuenca, Rafael. (2023). On the Prediction of Propeller Tonal Noise with Machine Learning. 10.26678/ABCM.COBEM2023.COB2023-1717.