Tutorial de Geração de Malha de um Bocal Axissimétrico
Geração de malha em bocal axissimétrico
Observações:
- Este tutorial tem função meramente didática, visando auxiliar usuários iniciantes, e não representa garantias de qualidade de resultados da simulação. A verificação e validação dos resultados, assim como estudos de refino de malha e demais análises, são de responsabilidade do usuário final.
- This offering is not approved or endorsed by OpenCFD Limited, producer and distributor of the OpenFOAM software via www.openfoam.com, and owner of the OPENFOAM® and OpenCFD® trade marks.
- Este tutorial foi criado dentro do contexto de um projeto de extensão da UFSC e não é homologado pelos desenvolvedores dos códigos GMESH e OpenFOAM®.
- Este tutorial foi elaborado pelo aluno de graduação Juliano Simon, sob supervisão de Filipe Dutra da Silva.
- Ao utilizar este material, solicita-se que sejam dadas as devidas referências à esta página. Dúvidas e sugestões podem ser enviadas aos endereços de contato da página.
Nesse tutorial será abordado o processo de criação de uma geometria e de uma malha estruturada para a simulação de escoamento em um bocal axissimétrico utilizando o código Gmsh.
O Gmsh pode ser utilizado de duas formas: através dos comandos da interface gráfica do programa ou editando o script, na forma do arquivo .geo, gerado pelo programa. Este tutorial abordará ambas as formas de uso do programa. Para abrir o script, vá para Modules→Geometry e clique em Edit script.
O primeiro passo é a declaração das coordenadas da geometria. No arquivo .geo digite as coordenadas da geometria no formato “Point(1) = (0,0,0,1.0);”, onde os primeiros três termos são as coordenadas x, y e z, respectivamente. Assim, o arquivo deve ficar dessa forma:
// DEFINIÇÂO DOS PONTOS: Point(1) = {-0.254,0,0,1.0}; Point(2) = {-0.199,0,0,1.0}; Point(3) = {0,0,0,1.0}; Point(4) = {2.496,0,0,1.0}; // Pontos do bocal: Point(5) = {-0.254,0.076,0,1.0}; Point(6) = {-0.199,0.076,0,1.0}; Point(7) = {-0.185,0.071,0,1.0}; Point(8) = {-0.139,0.047,0,1.0}; Point(9) = {-0.083,0.032,0,1.0}; Point(10) = {0,0.025,0,1.0}; Point(11) = {-0.254,0.077,0,1.0}; Point(12) = {-0.199,0.077,0,1.0}; Point(13) = {-0.185,0.072,0,1.0}; Point(14) = {-0.139,0.048,0,1.0}; Point(15) = {-0.083,0.033,0,1.0}; //----- Point(16) = {2.496,0.3762,0,1.0}; Point(17) = {-0.254,0.6,0,1.0}; Point(18) = {-0.199,0.608,0,1.0}; Point(19) = {0,0.6369,0,1.0}; Point(20) = {2.496,1,0,1.0}; //================================
Salve o arquivo. Na interface gráfica, clique em Modules→Geometry → Reload script (deverá ser pressionado sempre que for necessário aplicar as alteração feitas no.geo). O resultado é mostrado na figura abaixo.
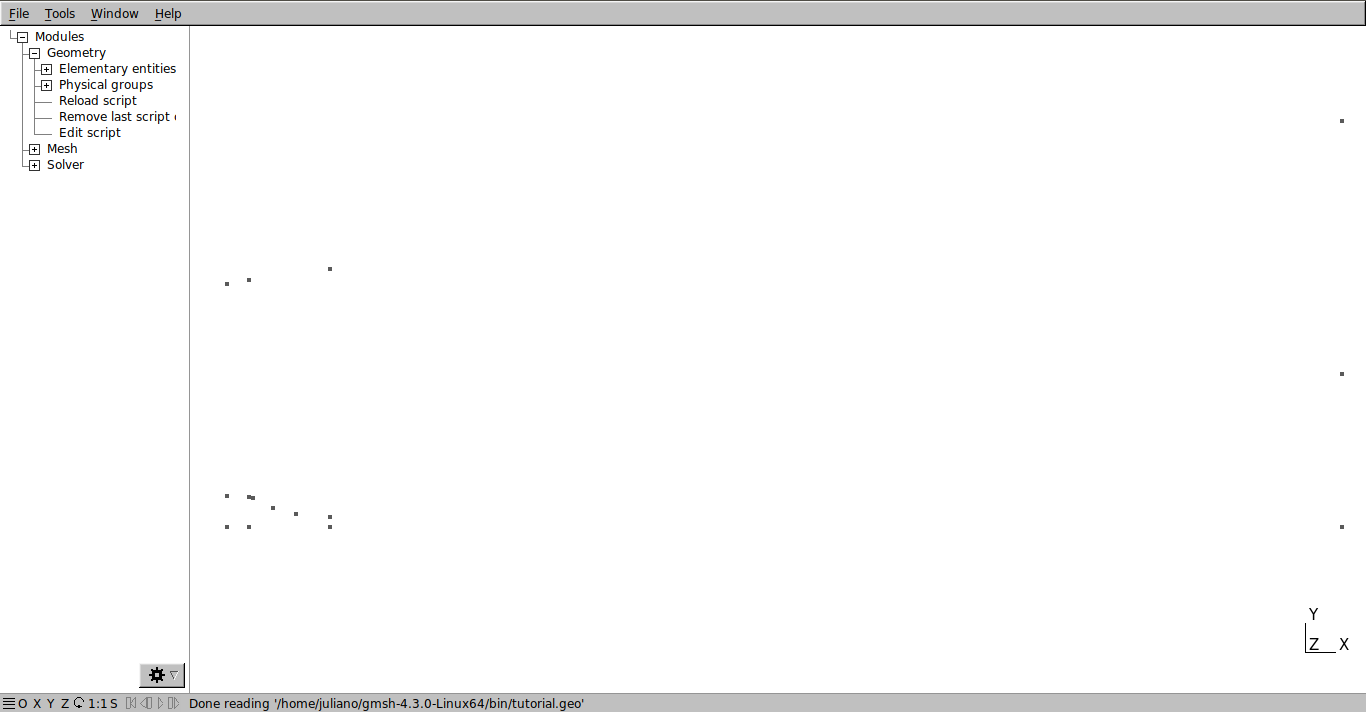
Obs: Para criar os pontos utilizando a interface gráfica, vá em Modules→Geometry → Elementary entities → Add → Point.
Note que os pontos que definem as superfícies interna e externa do bocal, no exemplo que está sendo construído, ficam bem próximos. A intenção é criar uma pequena espessura no bocal.
Mantenha consistência na numeração dos pontos. Não pode haver dois pontos com o mesmo nome e a numeração dos pontos é utilizada para criação das demais partes da geometria. Logo, a organização é fundamental para facilitar o trabalho. Caso seja necessário, pode-se tornar o nome dos pontos visíveis na interface gráfica em Tools → Options → Geometry e marcar a opção Point labels.
As linhas retas que definem o domínio da simulação e os blocos da malha podem ser geradas via script adicionando o comando “Line(1) = {1,2};”, onde 1 e 2 são os pontos que deseja-se conectar. Repita o processo até conectar todos os devidos pontos. O resultado no .geo e na interface deve ser como mostrado abaixo.
Obs: para unir os pontos na interface gráfica, utilize a ferramenta Modules→Geometry → Elementary entities → Add → Line e selecione os pontos que devem ser conectados.
// DEFINIÇÂO DAS LINHAS:
//+
Line(1) = {1, 2};
//+
Line(2) = {2, 3};
//+
Line(3) = {3, 4};
//+
Line(4) = {4, 16};
//+
Line(5) = {16, 20};
//+
Line(6) = {20, 19};
//+
Line(7) = {19, 18};
//+
Line(8) = {18, 17};
//+
Line(9) = {17, 11};
//+
Line(10) = {5, 1};
//+
Line(11) = {2, 6};
//+
Line(12) = {12, 18};
//+
Line(13) = {3, 10};
//+
Line(14) = {10, 19};
//+
Line(15) = {10, 16};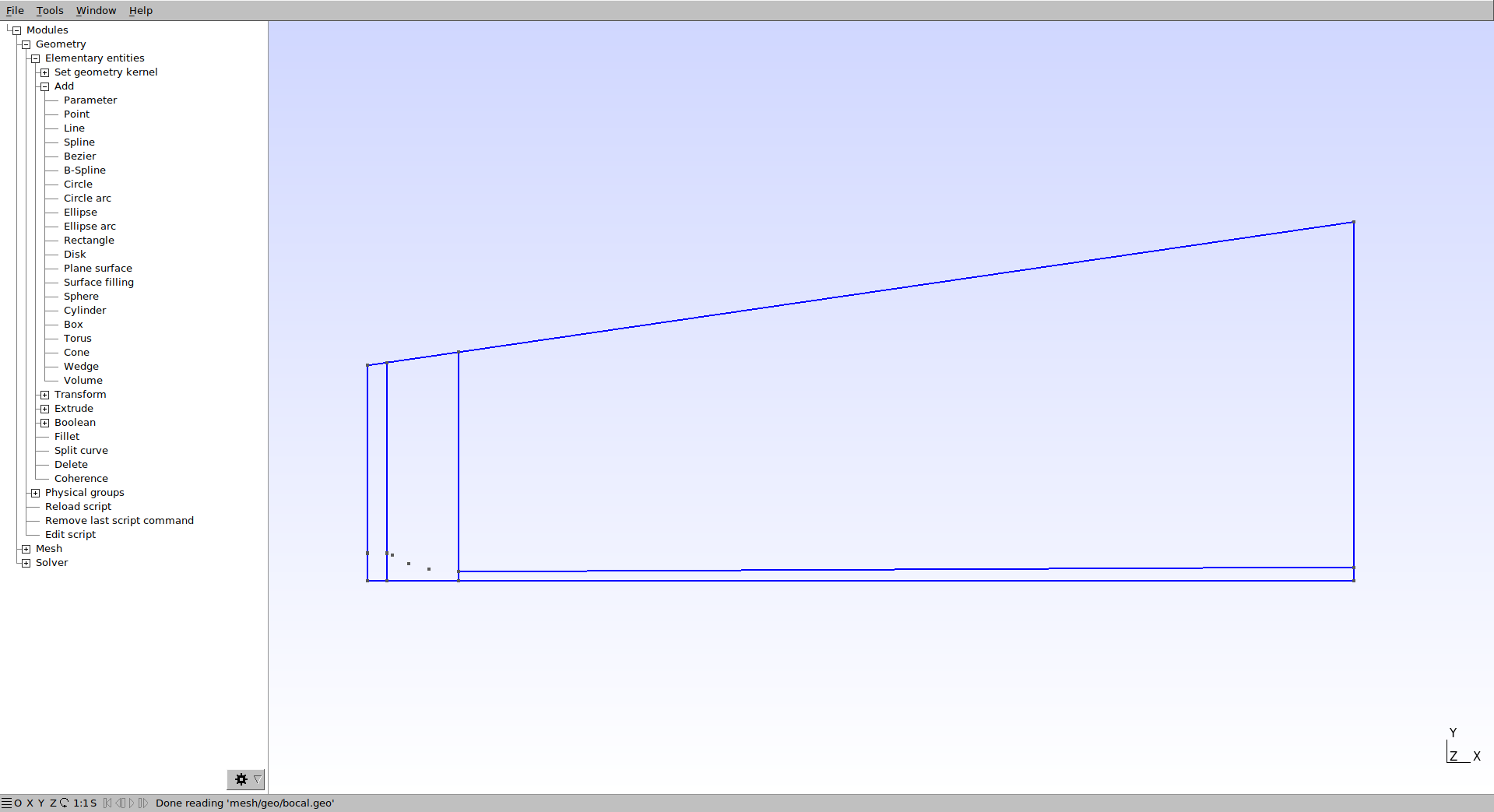
O contorno do bocal será definido em duas partes, a primeira com uma reta e a segunda com uma spline. As características da spline fazem com que talvez se torne necessário definir uma grande quantidade de pontos para que a forma se aproxime à do bocal que se deseja simular. Primeiramente conectamos os dois pontos da parte plana do bocal com uma linha.
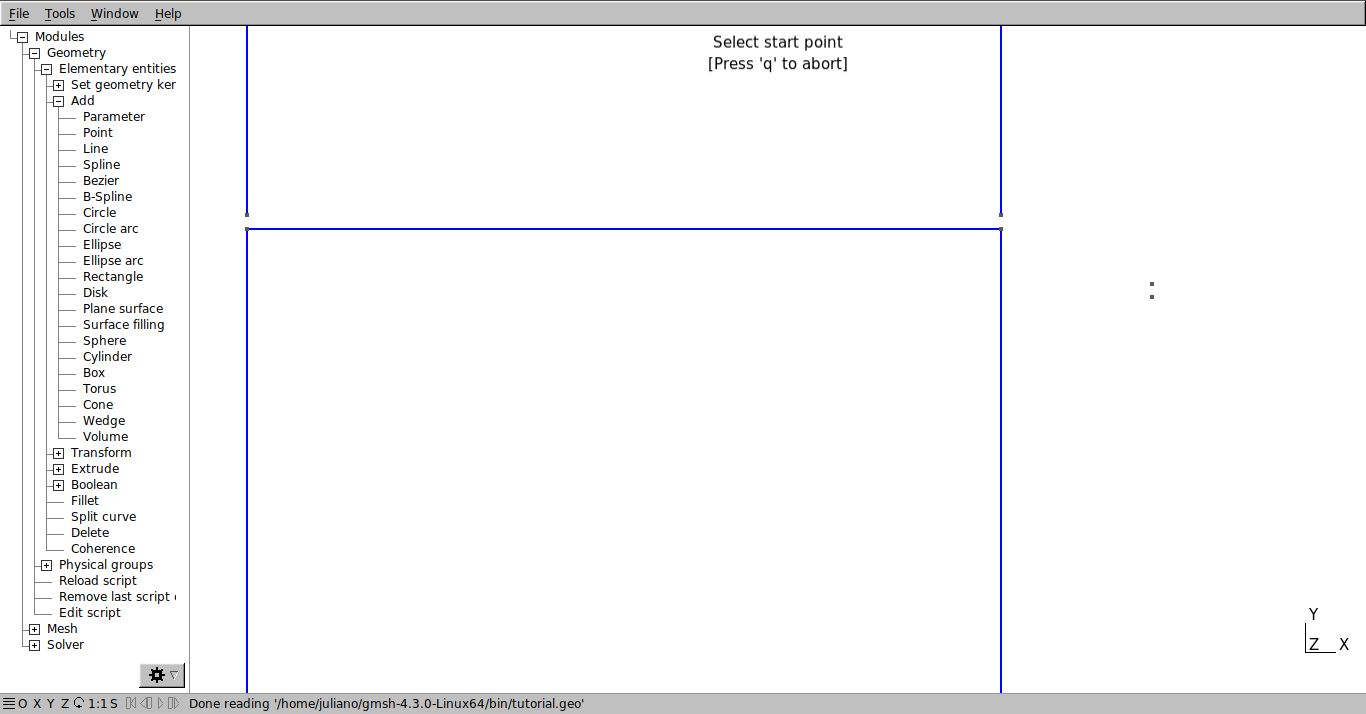
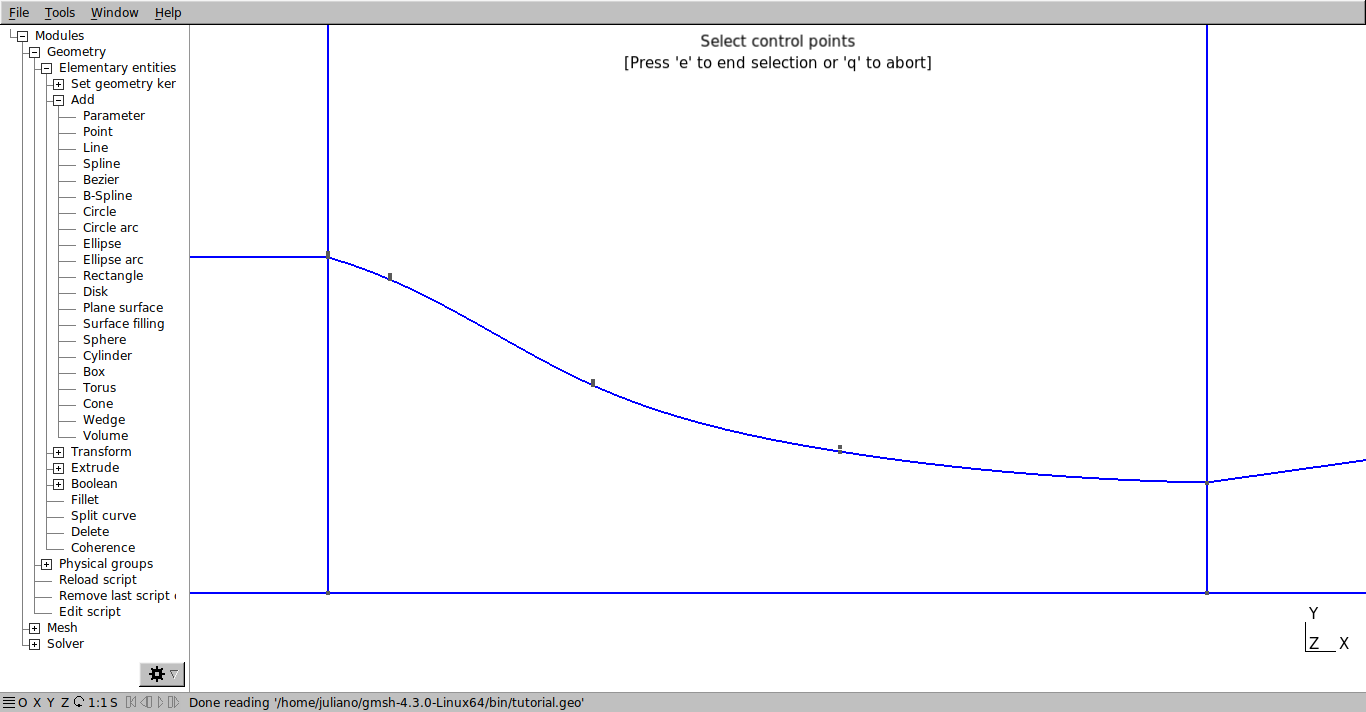
Para criar a spline no script digite “Spline(nº) = {6, 7, 8, 9, 10};” (sendo que a spline continua a numeração das linhas). Os números entre chaves representam os pontos que serão conectados na ordem que eles devem ser conectados.
Obs: Para definir a spline na interface gráfica vá em Modules→Geometry → Elementary entities → Add → Spline e selecione todos os pontos que deseja conectar e aperte a tecla “e” para confirmar.
Repita o mesmo processo com a parte externa do bocal.
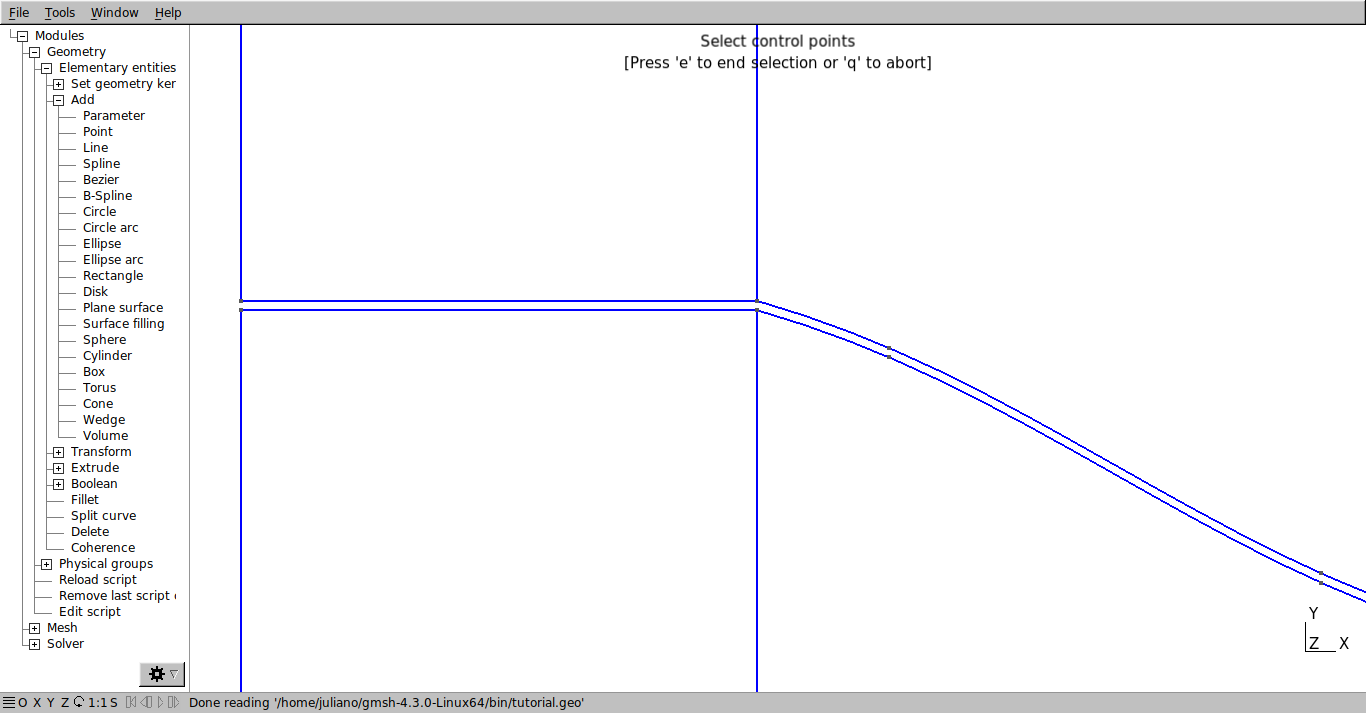
// Definição das linhas do bocal:
//+
Line(16) = {5, 6};
//+
Spline(17) = {6, 7, 8, 9, 10};
//+
Line(18) = {11, 12};
//+
Spline(19) = {12, 13, 14, 15, 10};
//================================
Em seguida, é hora de definir as superfícies. Para tal, selecione Modules→Geometry → Elementary entities → Add → Plane surface. Para definir uma superfície, quatro linhas devem ser selecionadas. Importante observar, que poderiam ser criadas superfícies entre três linhas ou mais. Contudo, como desejamos uma malha estruturada, as superfícies dos blocos da malha devem ser definidas desta forma. Isso explica as escolhas de repartição da geometria feitas anteriormente.
Selecione as quatro linhas que delimitarão cada superfície e aperte a tecla “e” para confirmar. Se o processo foi feito corretamente deverão aparecer linhas pontilhas no meio das superfícies.
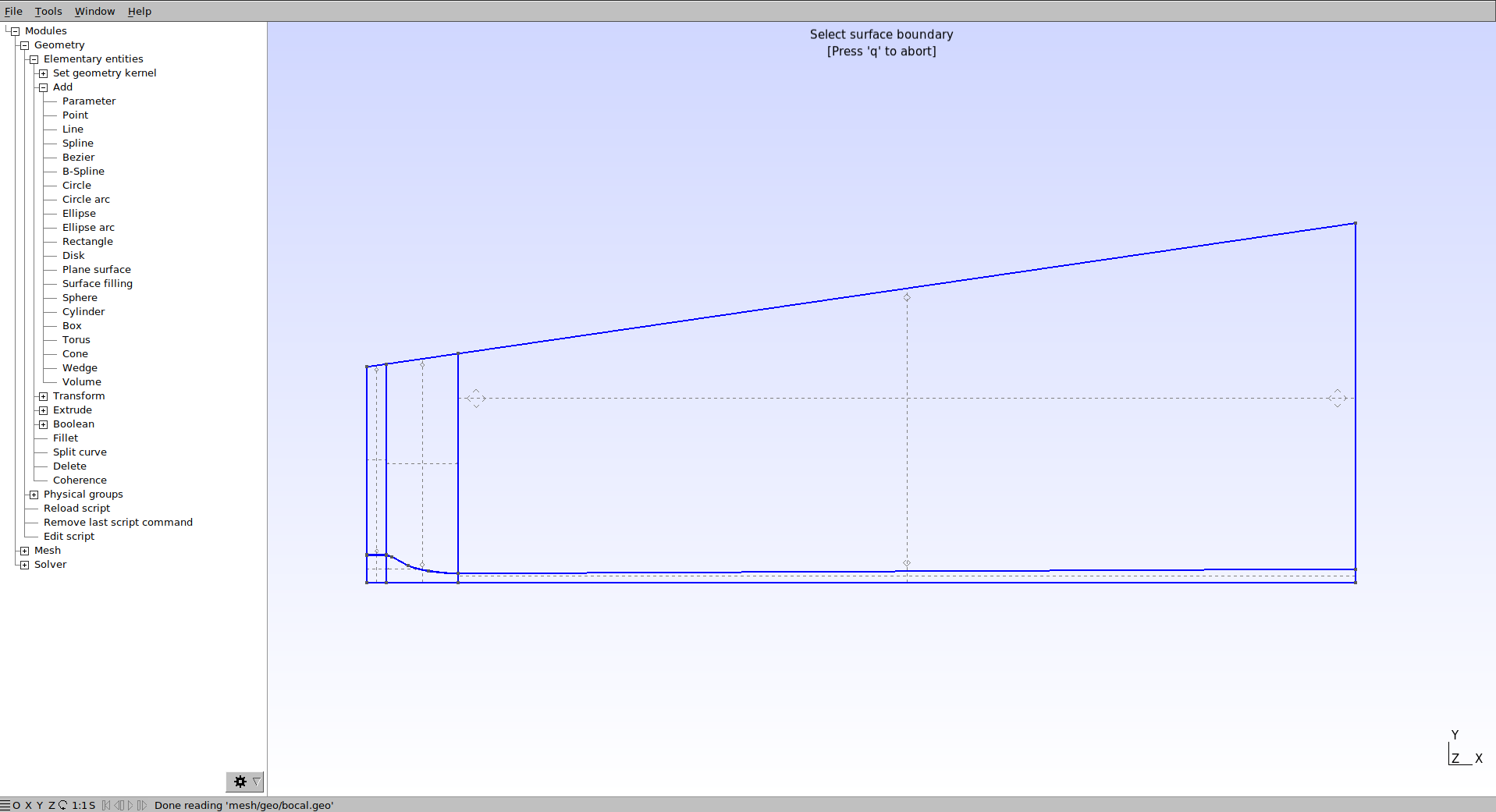
No script .geo, a definição da superfícies fica como demostrado abaixo.
//DEFINIÇÂO DAS SUPERFÍCIES:
//+
Curve Loop(1) = {1, 11, -16, 10};
//+
Plane Surface(1) = {1};
//+
Curve Loop(2) = {11, 17, -13, -2};
//+
Plane Surface(2) = {2};
//+
Curve Loop(3) = {13, 15, -4, -3};
//+
Plane Surface(3) = {3};
//+
Curve Loop(4) = {9, 18, 12, 8};
//+
Plane Surface(4) = {4};
//+
Curve Loop(5) = {12, -7, -14, -19};
//+
Plane Surface(5) = {5};
//+
Curve Loop(6) = {15, 5, 6, -14};
//+
Plane Surface(6) = {6};
//+
//================================
A função Curve Loop define as linhas que delimitam a superfície (os mesmos nomes das linhas anteriores) e a Plane Surface cria a superfície. Os sinais negativos no número de algumas linhas indicam as suas orientações, dependendo da ordem dos pontos que as definem.
Para a simulação axissimétrica no OpenFOAM, é necessário gerar um domínio na forma de cunha. Ainda, é necessário deixa o domínio simétrico em relação ao plano xy. Para tanto, é preciso rotacionar a malha base antes de gerar a cunha por extrusão.
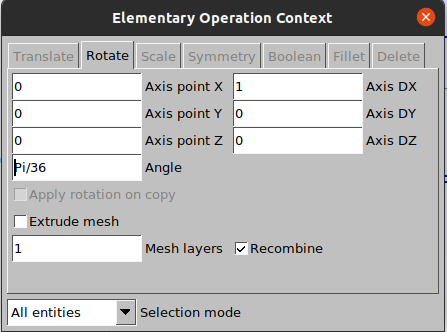
Clique em Modules→Geometry → Transform → Rotate e configure as opções segundo a figura abaixo.
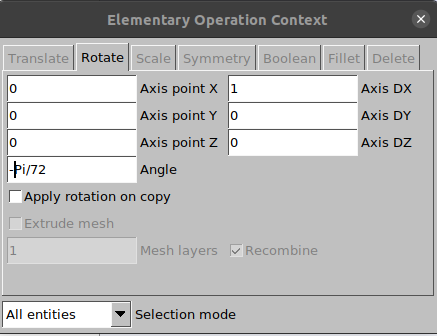
Selecione todas as faces e aperte a tecla “e” para confirmar a seleção.Dessa forma a geometria será rotacionada -2,5º para compensar a extrusão de 5º que será feita posteriormente.
No script a notação fica como mostrada abaixo:
// ROTAÇÃO:
Rotate {{1, 0, 0}, {0, 0, 0}, -Pi/72} {
Surface{1}; Surface{2}; Surface{3}; Surface{4}; Surface{5}; Surface{6};
}
//================================Para a criação de uma malha estruturada o Gmsh oferece a opção de Transfinite que deve ser aplicada em todas as linhas. Essa opção permitirá que você defina o número de volumes que sua malha terá, assim como a taxa de crescimento desses volumes ao longo de uma linha.
Clique em Modules → Mesh → Define → Transfinite → Curve. Será definido um Transfinite para cada linha, por isso é necessário que mantenha consistência na sua criação (pode-se deixar explícito o nome das linhas pelo mesmo caminho que foi utilizado
para os pontos) e a utilização de comentários no .geo para que não haja confusão com os nomes. Note que, por causa da rotação, o nome das linhas será diferente do que foi definido anteriormente. Selecione um linha e aperte a tecla “e” para confirmar. No .geo, a função será definida assim:
// TRANSFINITE:
//+
Transfinite Curve {20} = 10 Using Progression 1;
O valor 10 indica o número de divisões que a malha terá naquela linha e o valor um, a razão de tamanhos entre dois volumes consecutivos. Para facilitar a edição posterior desses valores, podemos substituí-los por variáveis.
// TRANSFINITE:
a=10;
//+
Transfinite Curve {20} = a Using Progression 1;ATENÇÃO: linhas opostas em um mesmo bloco devem ter o mesmo número de divisões para que a malha resultante seja estruturada, por isso é indicado colocar a mesma variável para estas linhas.
Para melhor organização, a criação das Tranfinites seguirá a seguinte ordem: primeiro as linhas horizontais internas do bocal, em seguida as linhas horizontais externas a frente do bocal, as linhas verticais internas, as linhas horizontais da parte eterna do bocal e as linhas verticais da parte externa do bocal. Caso esteja seguindo a mesma ordem do tutorial, o resultado deve ser como apresentado a seguir.
// TRANSFINITE:
// linha horizontais bocal interno:
a = 20;
b = 180;
//+
Transfinite Curve {20} = a Using Progression 1;
//+
Transfinite Curve {22} = a Using Progression 1;
//+
Transfinite Curve {26} = b Using Progression 1;
//+
Transfinite Curve {24} = b Using Progression 1;
// linhas horizontais frente bocal:
c = 225;
//+
Transfinite Curve {29} = c Using Progression 1;
//+
Transfinite Curve {27} = c Using Progression 1;
//+
Transfinite Curve {38} = c Using Progression 1;
// linha verticais interna bocal:
d = 40;
//+
Transfinite Curve {23} = d Using Progression 1;
//+
Transfinite Curve {21} = d Using Progression 1;
//+
Transfinite Curve {25} = d Using Progression 1;
//+
Transfinite Curve {28} = d Using Progression 1;
// linhas horizontais bocal externo:
e = 20;
f = 180;
//+
Transfinite Curve {31} = e Using Progression 1;
//+
Transfinite Curve {33} = e Using Progression 1;
//+
Transfinite Curve {36} = f Using Progression 1;
//+
Transfinite Curve {34} = f Using Progression 1;
// linhas verticais bocal externo:
g = 160;
//+
Transfinite Curve {30} = g Using Progression 1;
//+
Transfinite Curve {32} = g Using Progression 1;
//+
Transfinite Curve {35} = g Using Progression 1;
//+
Transfinite Curve {37} = g Using Progression 1;
Em seguida, é preciso aplicar um Transfinite nas superfícies. Clique em Modules → Mesh → Define → Transfinite → Surface. Selecione cada superfície e aperte a letra “e” para confirmar. Em seguida vá em Modules → Mesh → Define → Recombine e selecione todas as superfícies e aperte “e” para confirmar. O resultado no .geo deverá ser o mostrado abaixo.
//+
Transfinite Surface {1};
//+
Transfinite Surface {2};
//+
Transfinite Surface {3};
//+
Transfinite Surface {4};
//+
Transfinite Surface {5};
//+
Transfinite Surface {6};
//+
Recombine Surface {1, 2, 3, 4, 5, 6};
//=================================
De volta no programa a malha em 2D já pode ser visualizada clicando em Modules → Mesh → 2D e o resultado deve ser o mostrado a seguir.
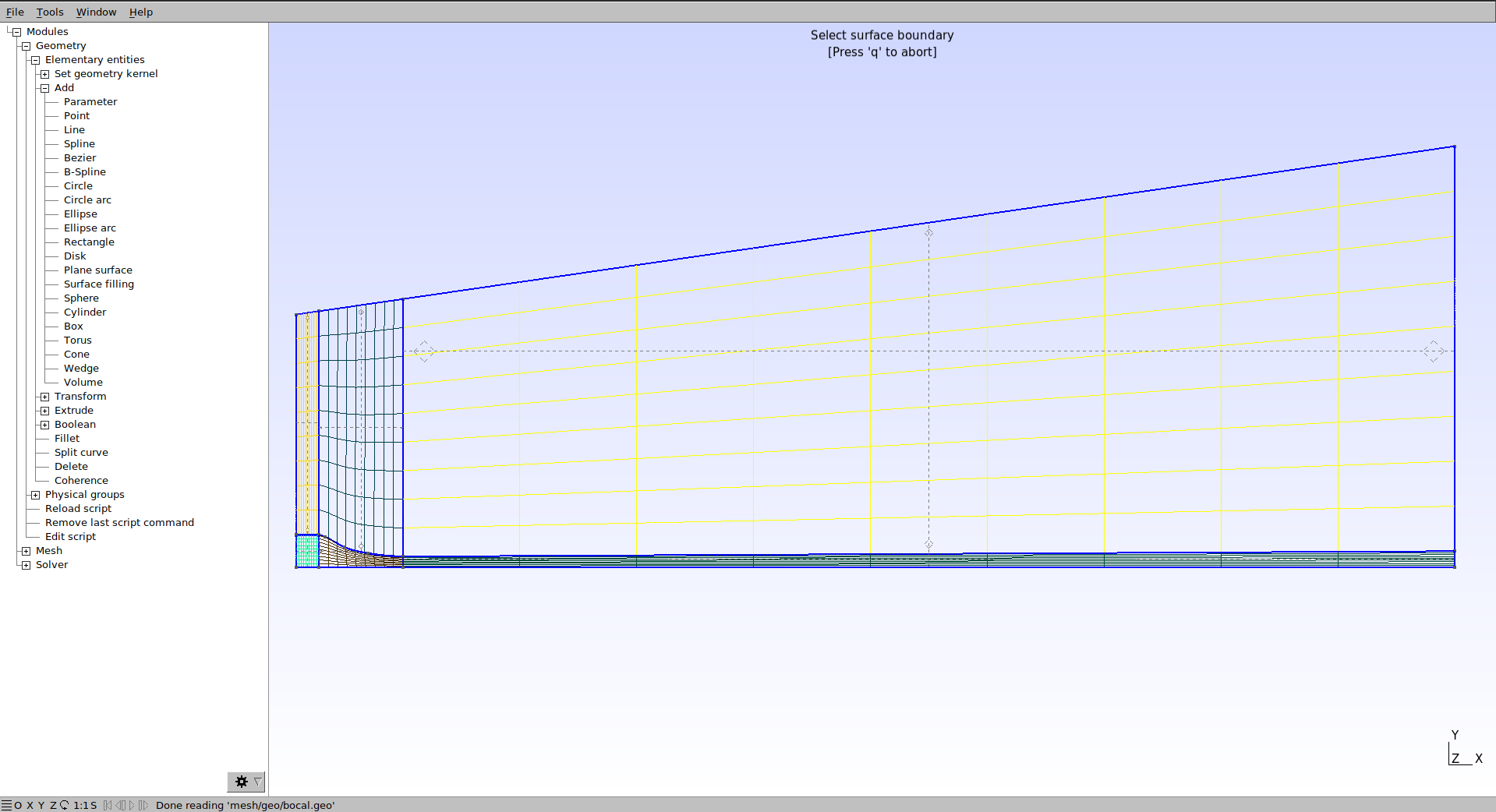
Caso a malha não estiver estruturada, refaça os passos anteriores.
Os valores da função Transfinite devem ser alterados para se obter o refino de malha necessário. Primeiramente mude a variável “a” para 20 e recarregue o Gmsh. Note que a quantidade de volumes da entrada do bocal irá aumentar.
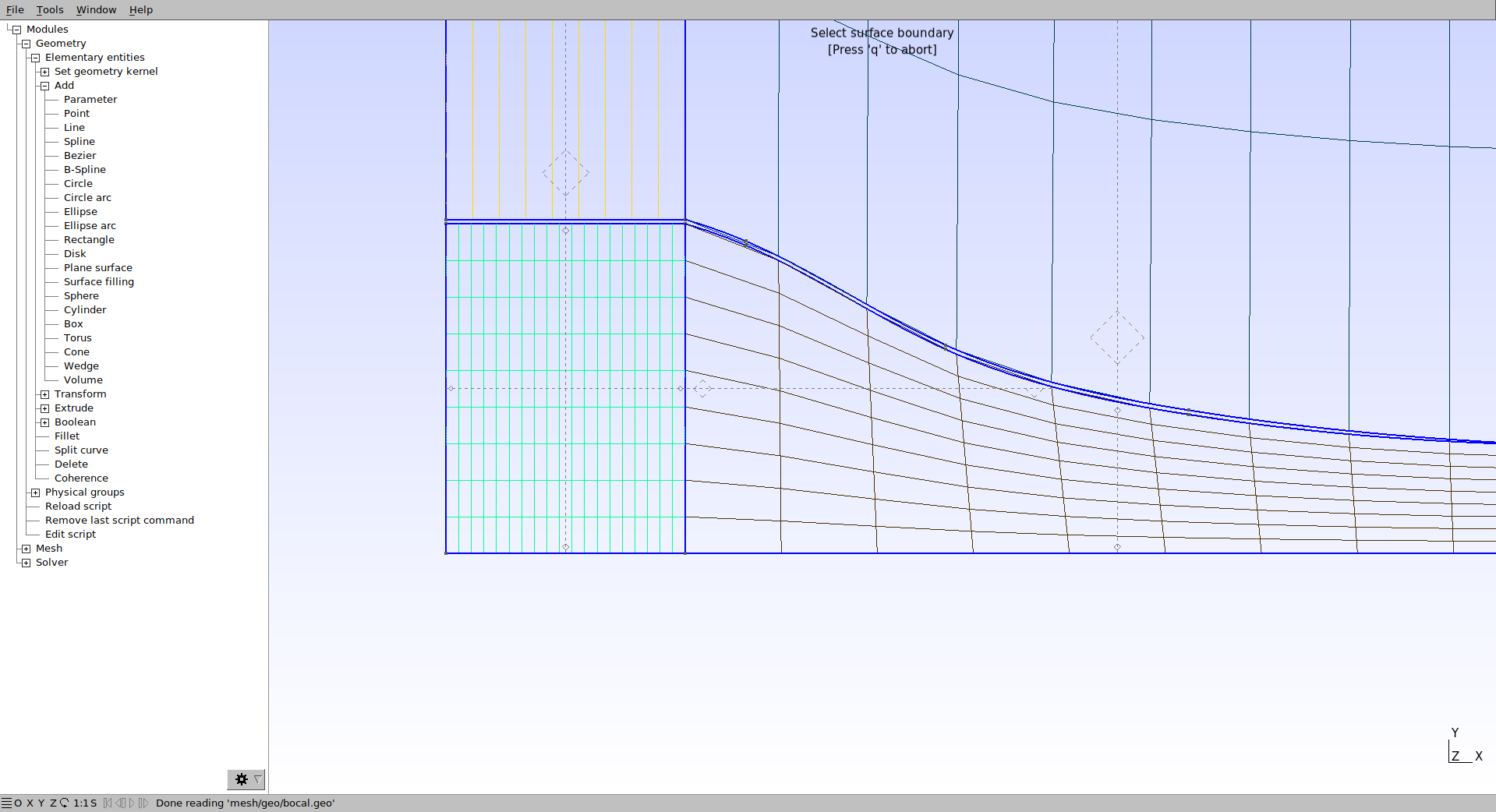
Em seguida altere b=180 , c= 225, d = 40, e=20, f=180 e g=160.
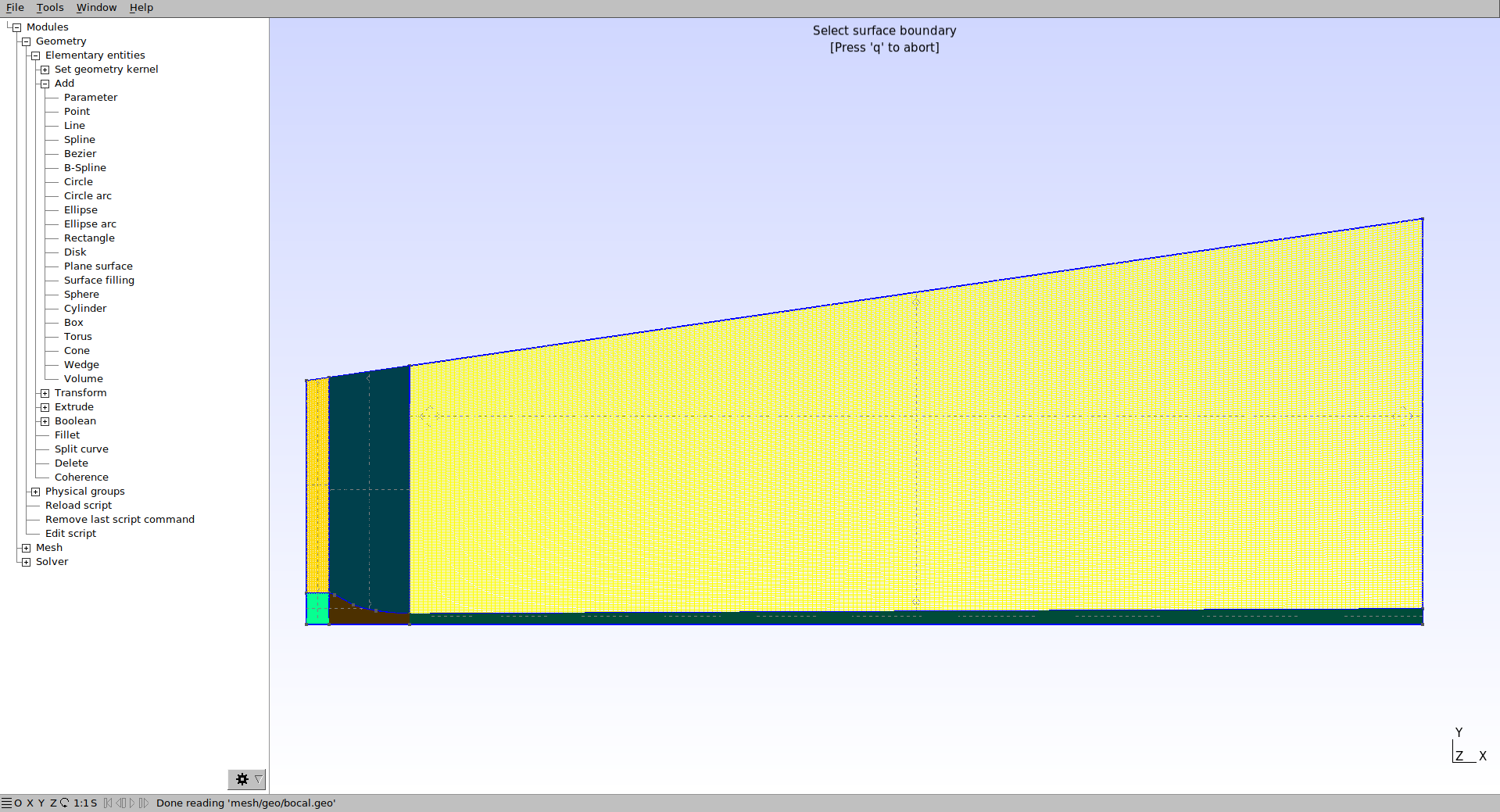
Agora deve-se mudar a taxa de crescimento dos volumes para que a malha fique mais refinada em certas regiões. Isso é feito alterando a variável “Progression” da função Transfinite. Primeiramente altere a taxa de crescimento da segunda divisão do bocal:
\\linhas horizontais bocal interno:
a = 20;
b = 180;
//+
Transfinite Curve {20} = a Using Progression 1;
//+
Transfinite Curve {22} = a Using Progression 1;
//+
Transfinite Curve {26} = b Using Progression 1/1.02;
//+
Transfinite Curve {24} = b Using Progression 1/1.02;
O resultado deve ser o mostrado a seguir:
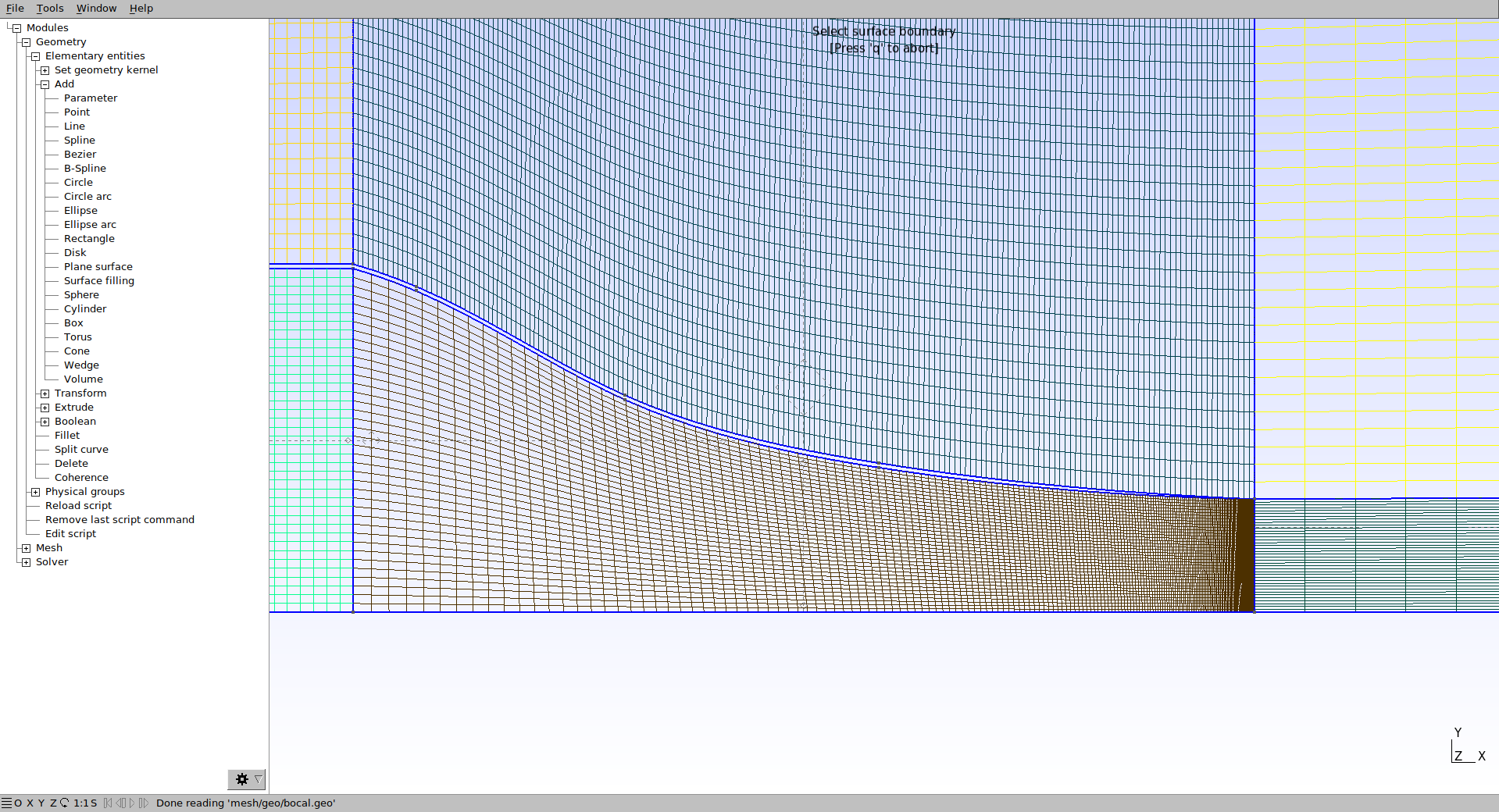
Note que foi escrito “1/1.027”, isso pois o essa taxa de crescimento segue a orientação de direção da linha, definida na sua criação. Caso a taxa de crescimento tenha ficado ao invertida pasta mudar para “1.027”. Em seguida, altere a taxa de crescimento das linhas horizontais na frente do bocal:
// linhas horizontais frente bocal:
c = 225;
//+
Transfinite Curve {29} = c Using Progression 1.027;
//+
Transfinite Curve {27} = c Using Progression 1.027;
//+
Transfinite Curve {38} = c Using Progression 1/1.027;
O resultado deverá ficar da seguinte forma:
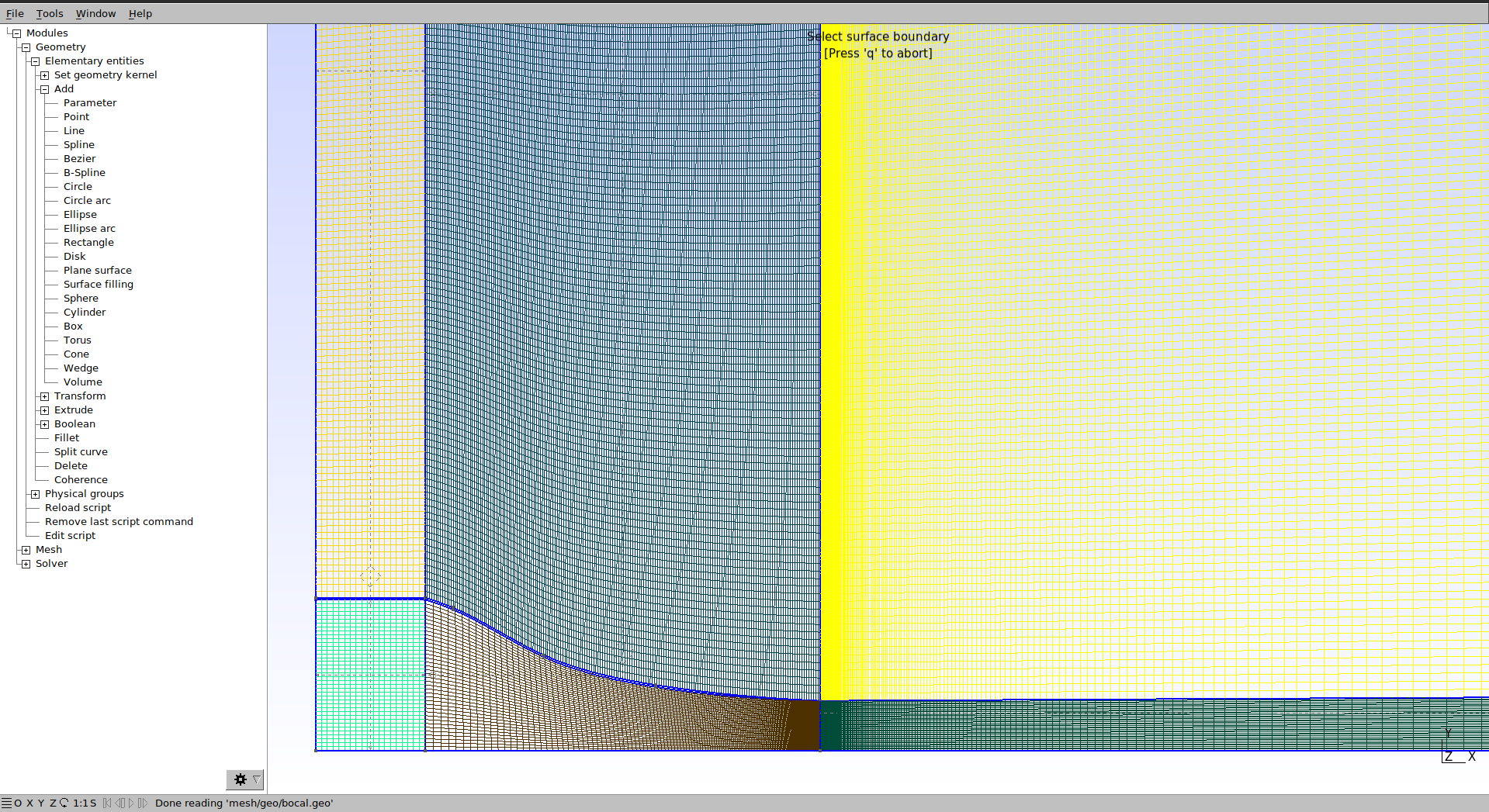
Altere agora a progressão das linhas verticais internas do bocal, para que a malha fique mais refinada na junto à parede:
// linhas verticais interna bocal:
d = 40;
//+
Transfinite Curve {23} = d Using Progression 1.025;
//+
Transfinite Curve {21} = d Using Progression 1/1.015;
//+
Transfinite Curve {25} = d Using Progression 1/1.01;
//+
Transfinite Curve {28} = d Using Progression 1.01;
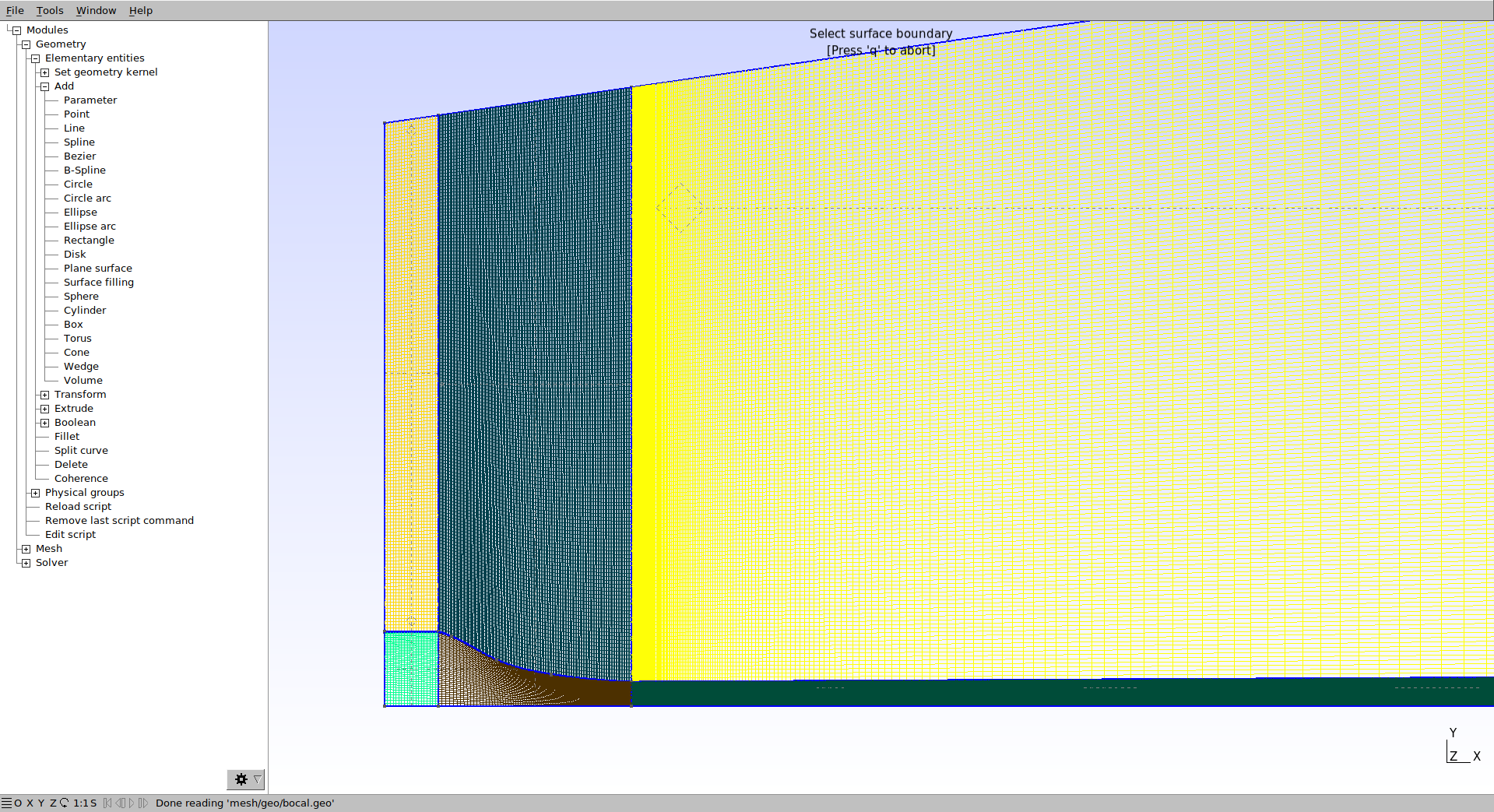
Na parte superior do bocal:
\\linhas horizontais bocal externo:
e = 20;
f = 180;
//+
Transfinite Curve {31} = e Using Progression 1;
//+
Transfinite Curve {33} = e Using Progression 1;
//+
Transfinite Curve {36} = f Using Progression 1/1.02;
//+
Transfinite Curve {34} = f Using Progression 1.027;

E por último as linhas verticais acima do bocal:
// linhas verticais bocal externo:
g = 160;
//+
Transfinite Curve {30} = g Using Progression 1/1.027;
//+
Transfinite Curve {32} = g Using Progression 1.027;
//+
Transfinite Curve {35} = g Using Progression 1.027;
//+
Transfinite Curve {37} = g Using Progression 1.027;
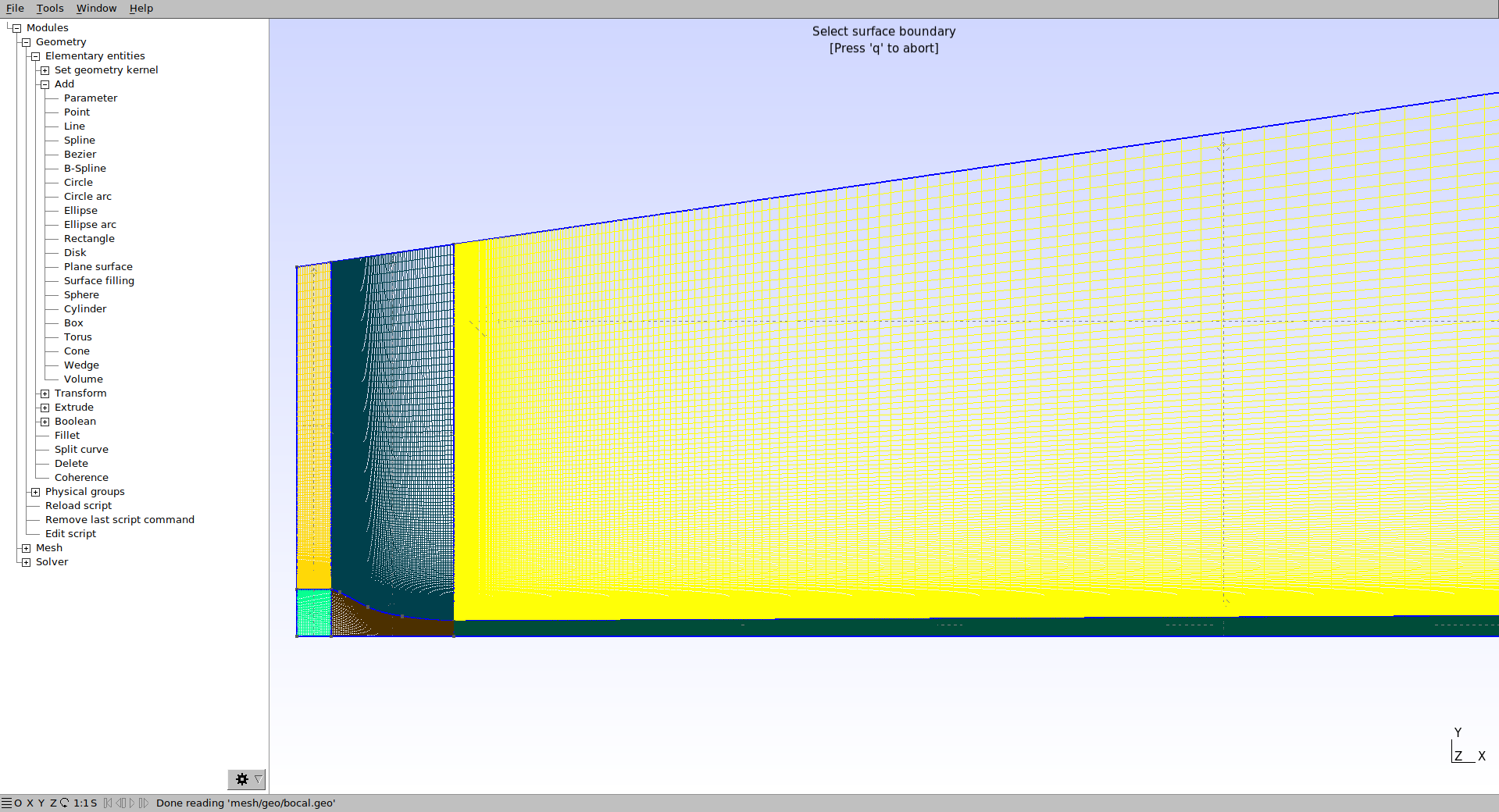
O passo seguinte é extrudar a geometria para ela ganhar a forma cunha. Este procedimento é necessário para rodar o caso com axissimetria no OpenFOAM. Para isso vá em Modules → Elementary entties → Extrude → Rotate e configure a janela como mostrado abaixo.
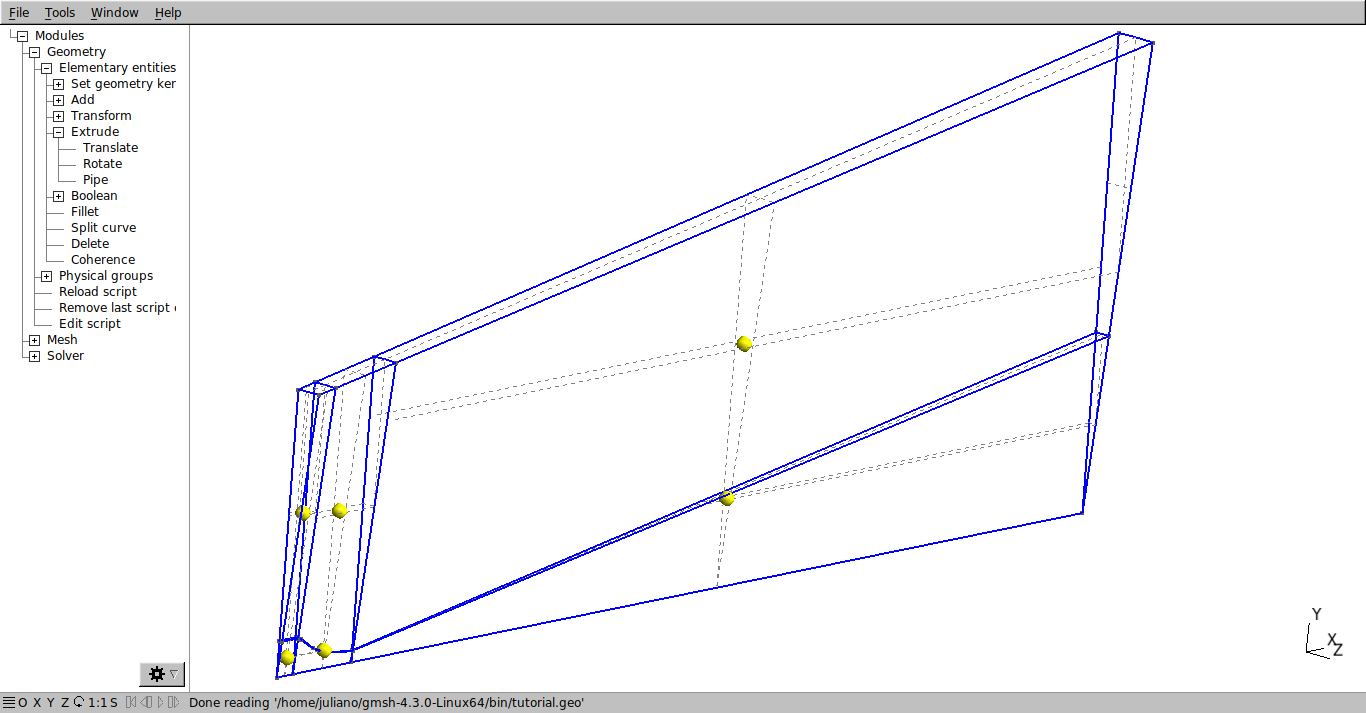
Em seguida, selecione todas as superfícies e aperte a tecla “e” para confirmar. O resultado deve se o mostrado a seguir.
Caso deseje fazer este processo via script, aplique as alterações a seguir na função Extrude do arquivo .geo
// EXTRUSÃO:
//+
Extrude {{1, 0, 0}, {0, 0, 0}, Pi/36} {
Surface{1}; Surface{2}; Surface{3}; Surface{4}; Surface{5}; Surface{6};
Layers{1};
Recombine;
}
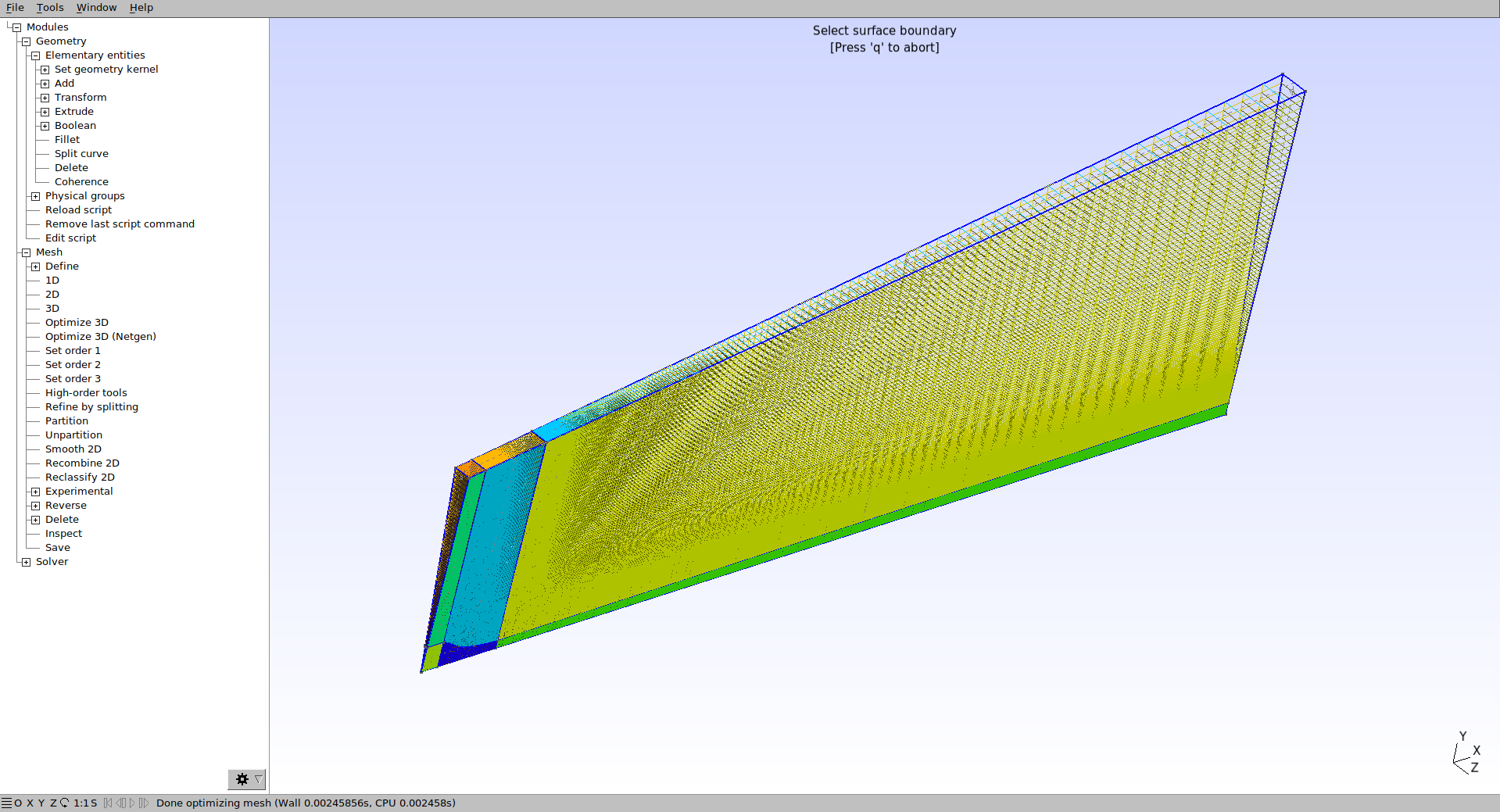
Agora já é possível visualizar a malha 3D clicando em Modules → Mesh → 3D. O resultado deve ser conforme mostrado a seguir. Caso a malha não esteja estruturada, revise os passos anteriores.
O último passo é definir os nomes das superfícies onde serão aplicadas as condições de contorno. Os nomes utilizados serão inlet, atmosphere, nozzle, wedge_1, wedge_2 e volume. Vá em Modules → Geometry → Physical Groups → Add → Surface. Nomeie “inlet”, selecione a superfície correspondente e aperte a letra “e”.
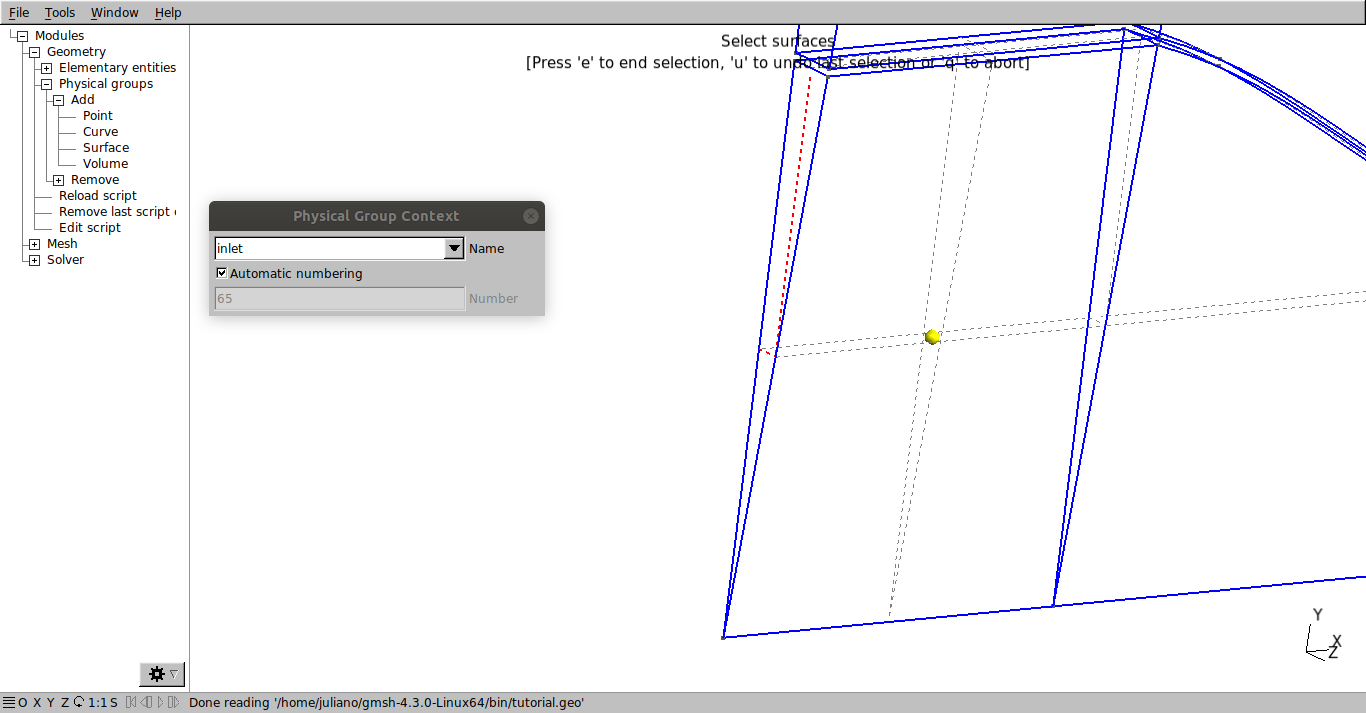
Faça o mesmo para as faces correspondentes a atmosfera, conforme a figura:
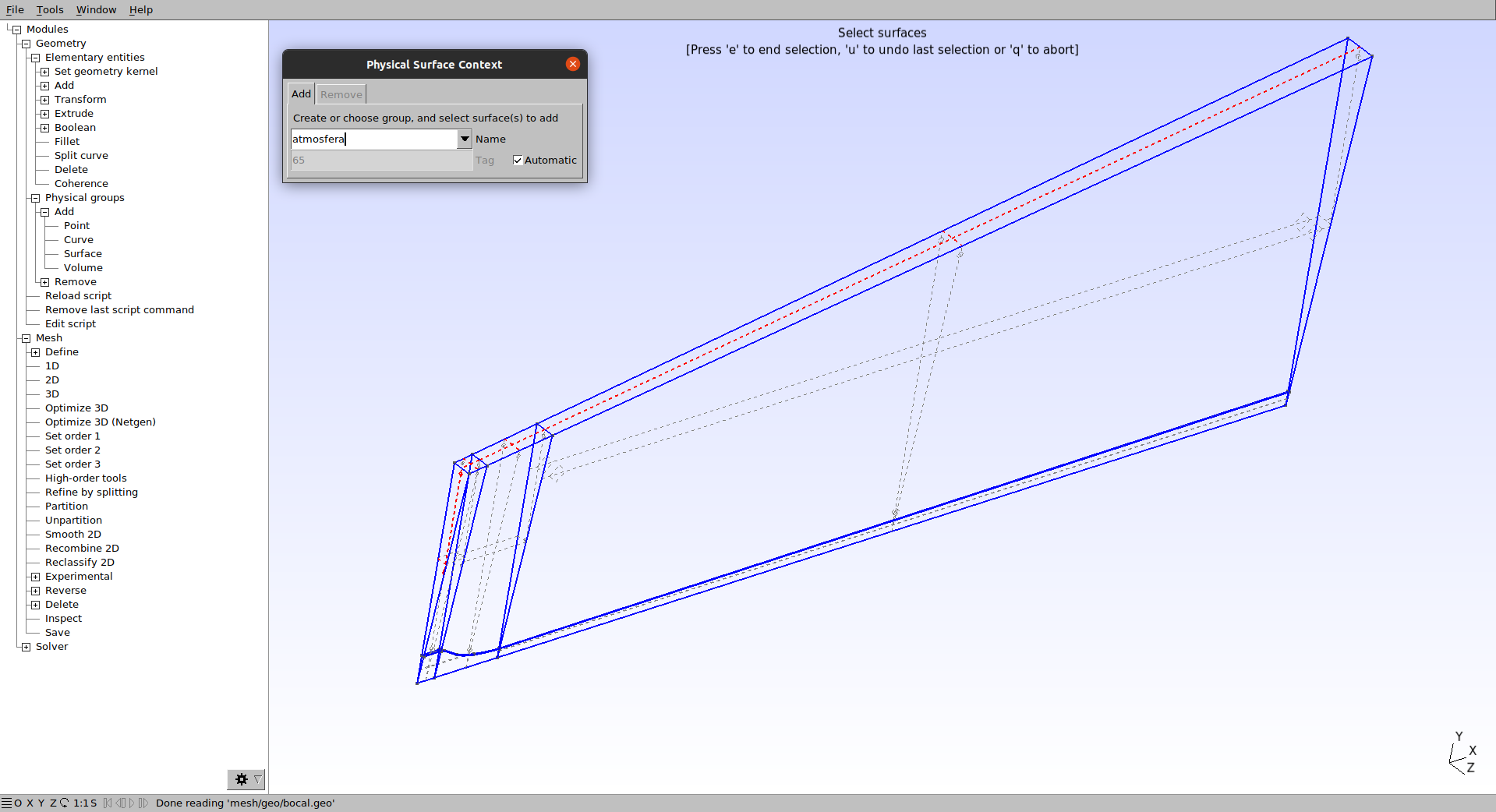
Repita o processo para as faces da parede do bocal:
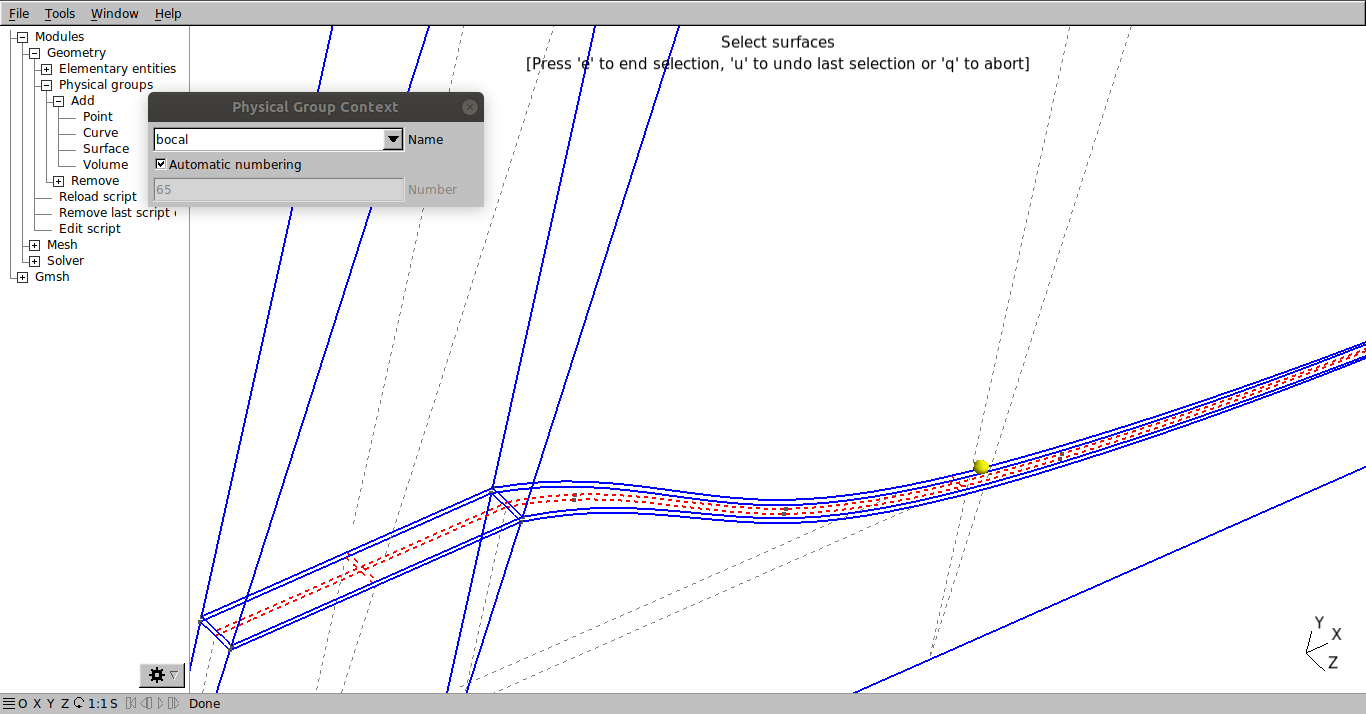
O wedge_1:
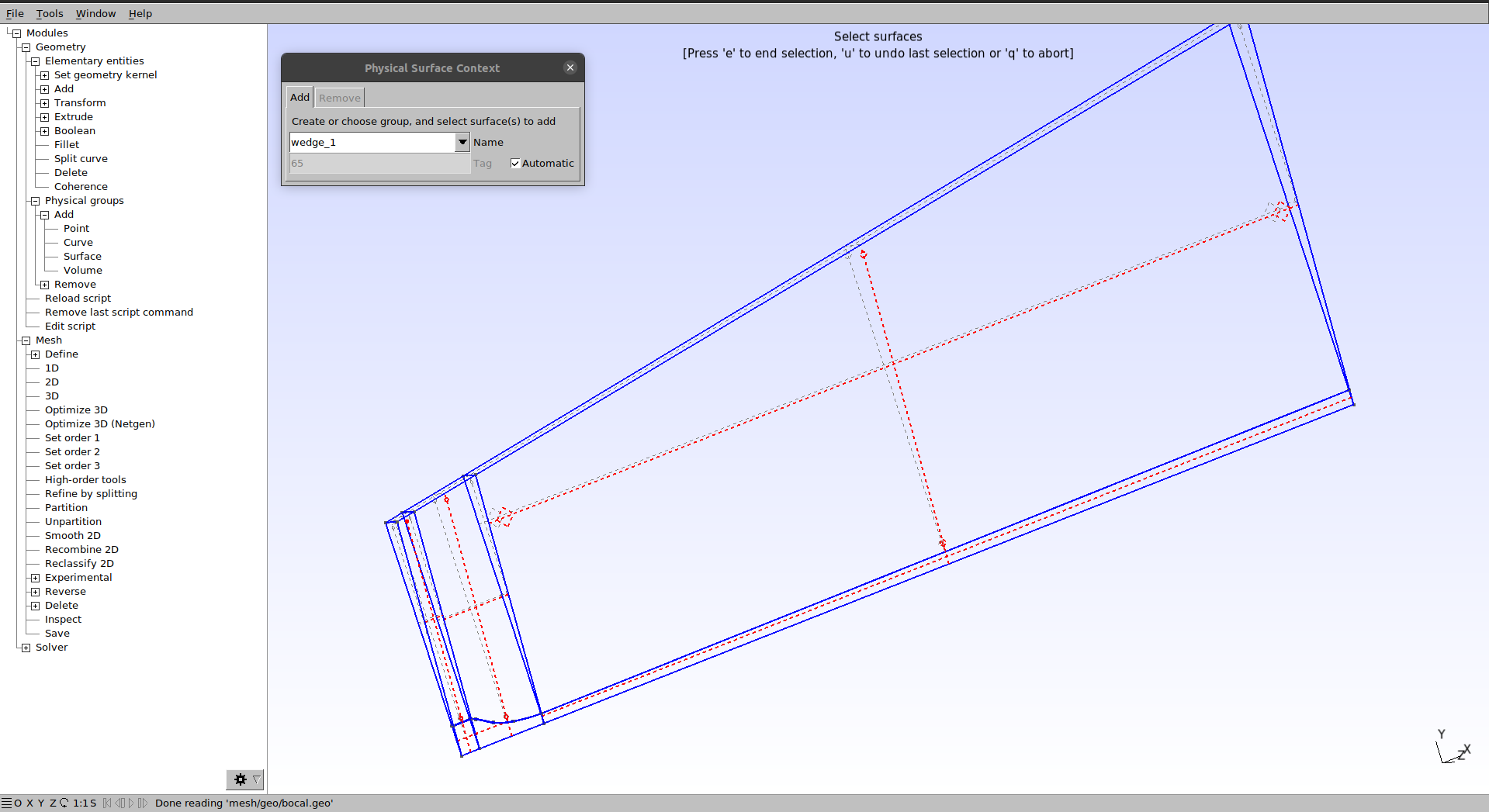
O wedge_2:
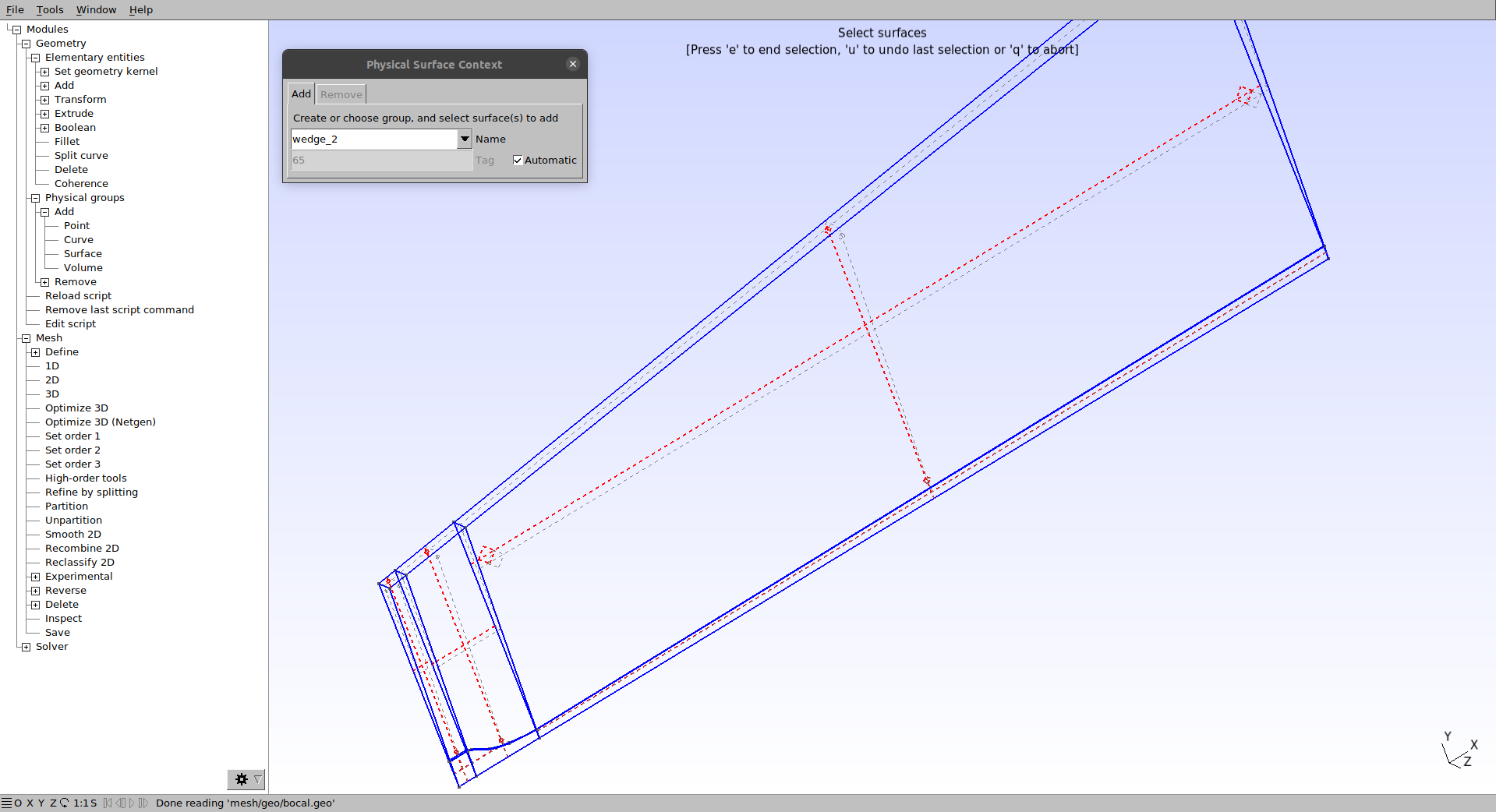
Vá em Modules → Geometry → Physical Groups → Add → Volume e selecione as esferas amarelas e pressione “e ” para confirmar:
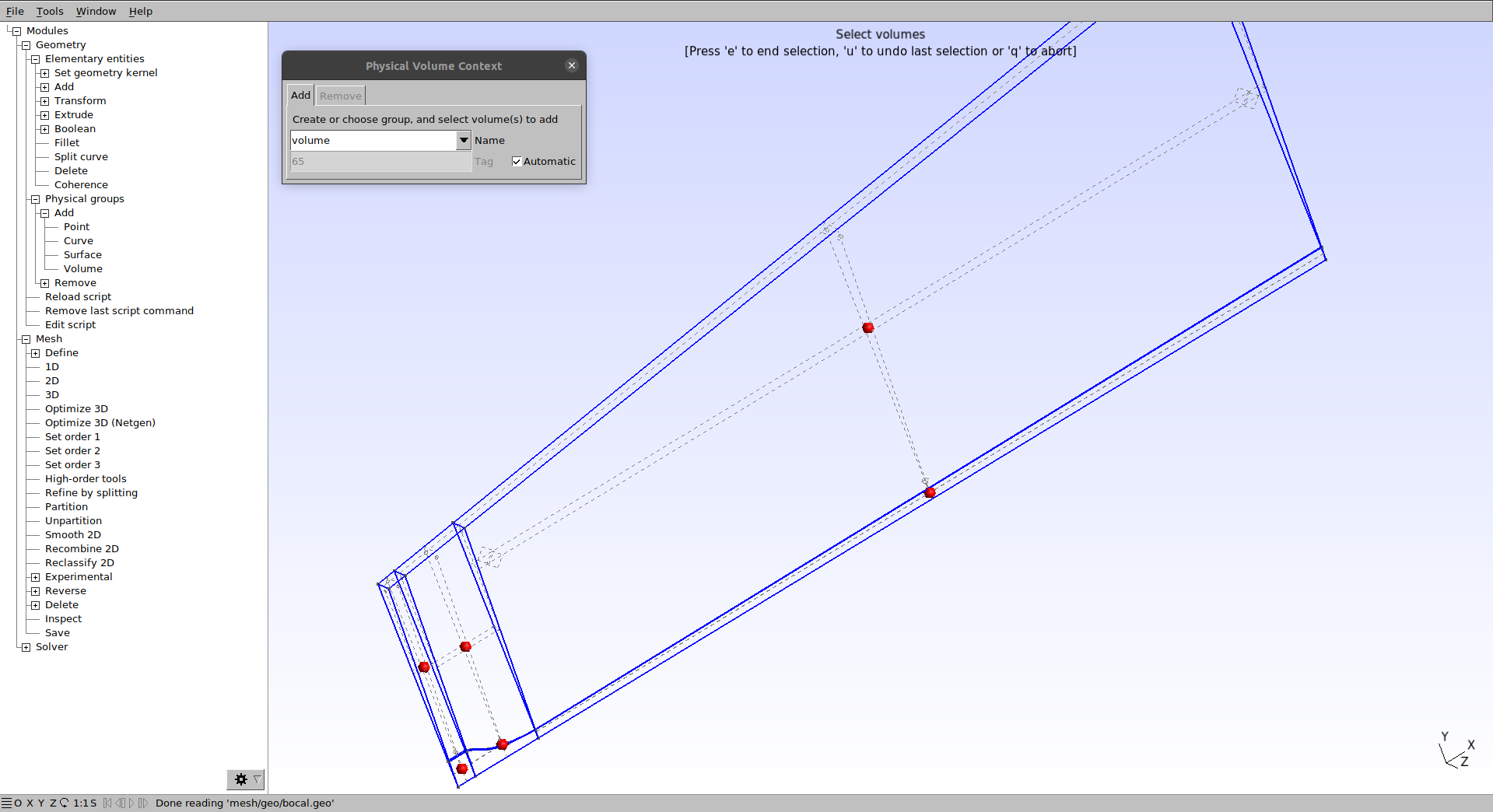
O resultado no .geo fica como o mostrado a seguir.
//+
Physical Surface("inlet") = {9};
//+
Physical Surface("atmosfera") = {17, 20, 22, 27, 26, 15};
//+
Physical Surface("bocal") = {18, 24, 11, 8};
//+
Physical Surface("wedge_1") = {10, 13, 16, 21, 25, 28};
//+
Physical Surface("wedge_2") = {1, 2, 3, 4, 5, 6};
//+
Physical Volume("volume", 65) = {1, 2, 3, 4, 5, 6};
Por último, Adicione o comando “Mesh 3;” no arquivo .geo e a criação da malha está completa. Para criar o arquivo que será utilizado no OpenFOAM clique em File → Export, escolha o local em que deseja salvar o arquivo e salve-o com a extensão .msh. Em seguida, aparecerá uma janela “MSH Options”, selecione para o formato “Version 2 ASCII” e aperte salvar. O arquivo de saída será utilizado para importação no OpenFOAM®.