Simulação de cilindros em tandem no OpenFOAM utilizando a biblioteca libAcoustics
Simulação de cilindros em tandem no OpenFOAM utilizando a biblioteca libAcoustics
Observações:
- Este tutorial tem função meramente didática, visando auxiliar usuários iniciantes, e não representa garantias de qualidade de resultados da simulação. A verificação e validação dos resultados, assim como estudos de refino de malha e demais análises, são de responsabilidade do usuário final.
- This offering is not approved or endorsed by OpenCFD Limited, producer and distributor of the OpenFOAM software via www.openfoam.com, and owner of the OPENFOAM® and OpenCFD® trade marks.
- Este tutorial foi criado dentro do contexto de um projeto de extensão da UFSC e não é homologado pelos desenvolvedores dos códigos GMSH, OpenFOAM® e LibAcoustics.
- Foi utilizada a versão 1912 do OpenFOAM.
- Este tutorial foi elaborado pelo aluno de graduação Julio Victor Vieira e Widmark Kauê Silva Cardoso sob supervisão de Filipe Dutra da Silva.
- Ao utilizar este material, solicita-se que sejam dadas as devidas referências à esta página. Dúvidas e sugestões podem ser enviadas aos endereços de contato da página.
Neste tutorial serão apresentados os passos para a simulação de um caso de cilindros em tandem no OpenFOAM juntamente com a biblioteca libAcoustics criada por Epikhin et al., utilizando um caso de dipolo 3D. Esta biblioteca contém a implementação de analogias acústicas que permitem o cálculo do ruído em campo distante a partir de dados aerodinâmicos coletados próximos à fonte. Primeiramente é calculada a pressão acústica no domínio do tempo. Em seguida, esses dados são convertidos para o domínio da frequência utilizando o algoritmo Fast Fourier Transform (FFT). Aqui faremos o uso da analogia de Ffowcs Williams-Hawkings (FWH) e da analogia Curle.
Obs: Antes de instalar a biblioteca libAcoustics, é necessário ter instalado a biblioteca FFTW.
Vamos utilizar como base um caso do próprio OpenFOAM e também um caso da biblioteca de acústica. Vá até o local onde o OpenFOAM está instalado e abra o seguinte diretório: tutorials/incompressible/pisoFoam/RAS. Copie a pasta “cavity” e cole onde você deseja salvar o tutorial com o nome “tutorialCilindros”.
Dentro de “tutorialCilindros” apague a pasta “system”, pois vamos utilizar um modelo de um caso da biblioteca de acústica. Abra, então, a pasta “Tutorials” que está junto com os arquivos de instalação da biblioteca libAcoustics. Abra o caso “dipole3D”, copie a pasta “system” e cole dentro da pasta “tutorialCilindros”.
O primeiro passo é importar a malha gerada previamente no Gmsh (Ver tutorial). Para isso, copie o arquivo “TandemCylinders.msh” e cole dentro da pasta “tutorialCilindros”. Assim, os seguintes arquivos devem ser vistos dentro da pasta:

Apague a pasta “system”, pois vamos utilizar um modelo de um caso da biblioteca de acústica. Abra, então, a pasta “Tutorials” que está junto com os arquivos de instalação da biblioteca libAcoustics (não confundir com a pasta “tutorials” do OpenFOAM). Abra o caso “dipole3D”, copie a pasta “system” e cole dentro da pasta “tutorialCilindros”.
Abra a pasta “constant” e dentro dela crie uma pasta com o nome “triSurface”. Agora copie as superfícies geradas no Gmsh (“superficie1.stl” e “superficie2.stl”) e cole dentro da pasta “triSurface”.
Em seguida, abra o terminal e vá até a pasta do caso. Digite “gmshToFoam TandemCylinders.msh” e aperte “enter”. Esse comando converte o formato da malha do Gmsh para o formato utilizado no OpenFOAM.

Agora digite “checkMesh” no terminal e aperte “enter”. Se tudo estiver certo com a malha, a mensagem “Mesh OK” deve aparecer.

O próximo passo é editarmos os arquivos do modelo copiado para as configurações do caso dos cilindros. Dentro da pasta “tutorialCilindros” abra a pasta “system”. Os arquivos que serão utilizados estão mostrados logo abaixo. Os demais arquivos podem ser excluídos.
Abra, então, o arquivo “controlDict”. Vamos utilizar o solver “pisoFoam”. Faça todas as modificações de acordo com as configurações mostradas abaixo:
application pisoFoam;
startFrom latestTime;
startTime 0;
stopAt endTime;
endTime 0.2;
deltaT 0.25e-4;
writeControl timeStep;
writeInterval 1000;
purgeWrite 0;
writeFormat ascii;
writePrecision 6;
writeCompression on;
timeFormat general;
timePrecision 6;
runTimeModifiable true;
adjustTimeStep false;
maxCo 2;
maxDeltaT 1e-3;
functions
{
#include "curleControl"
#include "fwhControl"
#include "soundPressureSampling"
}
Obs: em “functions” são inseridas as funções da biblioteca de aeroacústica.
Feitas as devidas mudanças, salve o arquivo “controlDict” e feche-o.
Ainda dentro da pasta “system”, abra o arquivo “fvSchemes”. Os seguintes esquemas numéricos serão utilizados (os demais esquemas que aparecem no modelo devem ser apagados):
ddtSchemes
{
default backward;
}
d2dt2Schemes
{
default Euler;
}
gradSchemes
{
default Gauss linear;
grad(p) Gauss linear;
grad(U) Gauss linear;
}
divSchemes
{
default Gauss limitedLinear 1;
div((nuEff*dev2(T(grad(U))))) Gauss linear;
}
laplacianSchemes
{
default Gauss linear corrected;
}
interpolationSchemes
{
default linear;
interpolate(U) linear;
}
snGradSchemes
{
default corrected;
}
fluxRequired
{
default no;
p ;
pcorr ;
}
wallDist
{
method meshWave;
}
Salve o arquivo “fvSchemes” e feche-o.
Agora, abra o arquivo “fvSolution”. Vamos usar as seguintes configurações:
solvers
{
p
{
solver PCG;
tolerance 1e-07;
relTol 1e-3;
preconditioner
{
preconditioner GAMG;
tolerance 1e-5;
relTol 0.01;
smoother GaussSeidel;
nPreSweeps 0;
nPostSweeps 2;
cacheAgglomeration no;
nCellsInCoarsestLevel 100;
agglomerator faceAreaPair;
mergeLevels 1;
}
}
pFinal
{
$p;
relTol 1e-6;
}
"(U|k|omega)"
{
solver smoothSolver;
smoother DILUGaussSeidel;
tolerance 1e-08;
relTol 0;
}
} PISO
{
nOuterCorrectors 1;
nCorrectors 3;
nNonOrthogonalCorrectors 1;
pRefCell 0;
pRefValue 0;
momentumPredictor true;
}
Salve as modificações feitas e feche o arquivo
Abra o arquivo “decomposeParDict”. Em “numberOfSubdomains” mude o valor para o número de processadores que você deseja utilizar em sua máquina para rodar a simulação em paralelo. Salve a mudança e feche o arquivo.
Agora abra o arquivo “curleControl”. Nele serão definidas as configurações da analogia Curle. Ele deve ser configurado da seguinte maneira:
CurleAnalogy
{
libs (“libAcoustics.so”);
type Curle;
log true;
probeFrequency 1;
patches (cyl-1 cyl-2);
timeStart 0.16;
timeEnd 0.2;
c0 343;
dRef -1;
pName p;
pInf 0;
rho rhoInf;
rhoInf 1.225;
CofR (0 0 0);
writeFft true;
U0 (44 0 0);
observers
{
microphone-A
{
position (-0.4761 1.5896 0.4572);
pRef 2.0e-5;
fftFreq 1024;
}
microphone-B
{
position (0.5206 1.8288 0.457);
pRef 2.0e-5;
fftFreq 1024;
}
microphone-C
{
position (1.5173 1.5896 0.457);
pRef 2.0e-5;
fftFreq 1024;
}
}
}
Em “patches” são especificadas as superfícies nas quais serão armazenadas os dados de entrada para a analogia de Curle , que nesse caso são as superfícies dos dois cilindros. Para pular o regime transiente, iniciamos a analogia apenas em 0.16 segundos. O “c0” indica a velocidade de propagação do som no ar. O “dRef” se refere à espessura do domínio para simulações 2D, mas como esse caso é 3D, ignoramos essa função alterando o seu valor para um número negativo. Por fim, temos em “observers” os pontos no campo distante em que serão medidos os níveis de ruído. O “fftFreq” indica a quantidade de dados presente em uma janela em que é aplicada a FFT.
Após fazer as modificações, salve e feche o arquivo “curleControl”.
Abra, então, o arquivo “fwhCommonSettings” para definir as configurações da analogia FWH. Vamos utilizar definições semelhantes a da analogia Curle. Para isso, substitua o conteúdo do arquivo pelo seguinte:
libs ("libAcoustics.so");
log true;
writeFft true;
probeFrequency 1;
timeStart 0.16;
timeEnd 0.2;
c0 343;
dRef -1;
pName p;
pInf 0;
rho rhoInf;
rhoInf 1.225;
CofR (0 0 0);
U0 (44 0 0);
observers
{
microphone-A
{
position (-0.4761 1.5896 0.4572);
pRef 2.0e-5;
fftFreq 1024;
}
microphone-B
{
position (0.5206 1.8288 0.457);
pRef 2.0e-5;
fftFreq 1024;
}
microphone-C
{
position (1.5173 1.5896 0.457);
pRef 2.0e-5;
fftFreq 1024;
}
}
Salve o arquivo “fwhCommonSettings” e feche-o.
Agora abra o arquivo “fwhControl”. Para a analogia Curle as superfícies utilizadas para a aquisição dos dados são as próprias superfícies dos cilindros (definidas em “patches” no arquivo “curleControl”). Já para a analogia FWH as superfícies a serem utilizadas são aquelas geradas no Gmsh no formato .stl e inseridas na pasta /constant/triSurface. As configurações dessas superfícies são definidas no arquivo “fwhControl”. Substitua seu conteúdo pelo seguinte:
superficie1
{
type FfowcsWilliamsHawkings;
#include "fwhCommonSettings";
patches (cyl-1 cyl-2);
formulationType GTFormulation;
cleanFreq 100;
interpolationScheme insideCells;
surfaces
(
superficie1
{
type sampledTriSurfaceMesh;
surface superficie1.stl;
source insideCells;
interpolate false;
}
);
nonUniformSurfaceMotion false;
Ufwh (0 0.0 0.0);
fixedResponseDelay true;
responseDelay 1e-6;
}
superficie2
{
type FfowcsWilliamsHawkings;
#include "fwhCommonSettings";
patches (cyl-1 cyl-2);
formulationType GTFormulation;
cleanFreq 100;
interpolationScheme insideCells;
surfaces
(
superficie2
{
type sampledTriSurfaceMesh;
surface superficie2.stl;
source insideCells;
interpolate false;
}
);
nonUniformSurfaceMotion false;
Ufwh (0.0 0.0 0.0);
fixedResponseDelay true;
responseDelay 1e-6;
}
As superfícies de aquisição em “surfaces” são aquelas dentro da pasta “triSurface” e não as superfícies dos cilindros. O “Ufwh” é utilizado quando se deseja uma superfície móvel, porém nesse caso vamos utilizar superfícies estacionárias.
Feitas as alterações, salve o arquivo “fwhControl” e feche-o.
O último arquivo pertencente à biblioteca é o “soundPressureSampling”. Abra-o e substitua seu conteúdo pelo mostrado abaixo. Nele são configuradas os dados que as superfícies devem coletar e também a forma em que devem ser salvos.
surfacePressure{type soundPressureSampler;libs (“libAcoustics.so”);writeControl timeStep;writeInterval 1;outputGeometryFormat gmsh; fields ( p ); pName p; log true; interpolationScheme cellPoint; surfaces ( superficie1 { type sampledTriSurfaceMesh; surface superficie1.stl; source cells; interpolate true; } superficie2 { type sampledTriSurfaceMesh; surface superficie2.stl; source cells; interpolate true; } );}
Após aplicar as mudanças, salve e feche o arquivo.
As configurações dos arquivos na pasta “system” estão concluídas. Volte para o diretório do “tutorialCilindros” e abra a pasta “constant” e depois abra o arquivo “transportProperties”. Nele, insira a viscosidade e a densidade do ar, como mostrado abaixo.
transportModel Newtonian;nu nu [ 0 2 -1 0 0 0 0 ] 1.47e-05;
rho rho [ 1 -3 0 0 0 0 0 ] 1.225;
rho [ 1 -3 0 0 0 0 0 ] 1.225;Ainda na pasta “constant”, abra o arquivo “turbulenceProperties”. O modelo de turbulência a ser utilizado é o “kOmegaSST”.
simulationType RAS;
RAS{
RASModel kOmegaSST;
turbulence on;
printCoeffs on;
}Salve as mudanças e feche o arquivo.
Vá até a pasta “polyMesh” e abra o arquivo “boundary”. Vamos alterar o tipo da face dos dois cilindros para parede. Para fazer isso, troque o “type” e “physicalType” de “patch” para “wall” em ambos os cilindros. As demais configurações permanecem inalteradas, como mostradas abaixo.
6
(
frontAndBack
{
type patch;
physicalType patch;
nFaces 39536;
startFace 569932;
}
free
{
type patch;
physicalType patch;
nFaces 3320;
startFace 609468;
}
inlet
{
type patch;
physicalType patch;
nFaces 1120;
startFace 612788;
}
outlet
{
type patch;
physicalType patch;
nFaces 1120;
startFace 613908;
}
cyl-1
{
type wall;
physicalType wall;
nFaces 560;
startFace 615028;
}
cyl-2
{
type wall;
physicalType wall;
nFaces 560;
startFace 615588;
}
)Salve o arquivo “boundary” e feche-o. Retorne para o diretório do “tutorialCilindros”.
Por fim, vamos definir as condições de contorno. Abra a pasta “0”. Os arquivos “epsilon” e “nuTilda” devem ser excluídos, restando apenas os arquivos mostrados logo abaixo.
Substitua o conteúdo de cada arquivo conforme mostrado abaixo.
“k” :
dimensions [0 2 -2 0 0 0 0];
internalField uniform 0.00325;
boundaryField
{
inlet
{
type freestream;
freestreamValue $internalField;
}
outlet
{
type zeroGradient;
}
cyl-1
{
type kqRWallFunction;
value uniform 0.00325;
}
cyl-2
{
type kqRWallFunction;
value uniform 0.00325;
}
free
{
type freestream;
freestreamValue $internalField;
}
frontAndBack
{
type zeroGradient;
}
}
“nut” :
dimensions [0 2 -1 0 0 0 0];
internalField uniform 0;
boundaryField
{
inlet
{
type calculated;
value uniform 0;
}
outlet
{
type calculated;
value uniform 0;
}
cyl-1
{
type nutUSpaldingWallFunction;
value uniform 0;
}
cyl-2
{
type nutUSpaldingWallFunction;
value uniform 0;
}
free
{
type calculated;
value uniform 0;
}
frontAndBack
{
type zeroGradient;
}
}“omega” :
dimensions [0 0 -1 0 0 0 0];
internalField uniform 43;
boundaryField
{
inlet
{
type freestream;
freestreamValue $internalField;
}
outlet
{
type zeroGradient;
}
cyl-1
{
type omegaWallFunction;
value $internalField;
}
cyl-2
{
type omegaWallFunction;
value $internalField;
}
free
{
type freestream;
freestreamValue $internalField;
}
frontAndBack
{
type zeroGradient;
}
}Obs.: utilizamos função parede nos cilindros para cada um dos arquivos acima.
“p” :
dimensions [0 2 -2 0 0 0 0];
internalField uniform 0;
boundaryField
{
inlet
{
type freestreamPressure;
freestreamValue uniform 0;
}
outlet
{
type fixedValue;
value uniform 0;
}
cyl-1
{
type zeroGradient;
}
cyl-2
{
type zeroGradient;
}
free
{
type freestreamPressure;
freestreamValue uniform 0;
}
frontAndBack
{
type zeroGradient;
}
}“U” :
dimensions [0 1 -1 0 0 0 0];internalField uniform (44 0 0);
boundaryField
{
inlet
{
type freestreamVelocity;
freestreamValue uniform (44 0 0);
}
outlet
{
type zeroGradient;
}
cyl-1
{
type noSlip;
}
cyl-2
{
type noSlip;
}
free
{
type freestreamVelocity;
freestreamValue uniform (44 0 0);
}
frontAndBack
{
type slip;
}
}Obs: Para a pressão na entrada utilizamos a pressão de corrente livre. Para a velocidade, utilizamos a condição de não escorregamento em ambos os cilindros.
Já podemos iniciar a simulação. Abra o terminal e vá até o diretório do caso “tutorialCilindros”. Primeiro vamos decompor o domínio para rodar em paralelo. Digite “decomposePar” no terminal.

Em seguida digite “mpirun -np 5 pisoFoam -parallel > log &” para rodar a simulação (substitua o número 5 pela quantidade de processadores configurados no arquivo “decomposeParDict”).

Obs: A simulação pode demorar algumas horas. Os detalhes do processo vão sendo registrados no arquivo “log” dentro da pasta “tutorialCilindros”.
Pós-processamento
Terminada a simulação, digite “reconstructPar -latestTime” no terminal para obter o último passo da simulação.

Para verificar o valor de y+, digite “pisoFoam -postProcess -func yPlus”.

Antes de abrir os resultados no Paraview, é necessário criar um arquivo com a extensão .foam. Para isso, digite “nano cilindros.foam” e aperte “enter”. Em seguida aperte “ctrl + o”, “enter” e por fim “ctrl + x”.

Para abrir o Paraview digite “paraview cilindros.foam”

No Paraview, clique em Apply. Para visualizar o campo de pressão, primeiro selecione o último passo de tempo e também clique na opção “Rescale to data range” como indicado na figura abaixo.
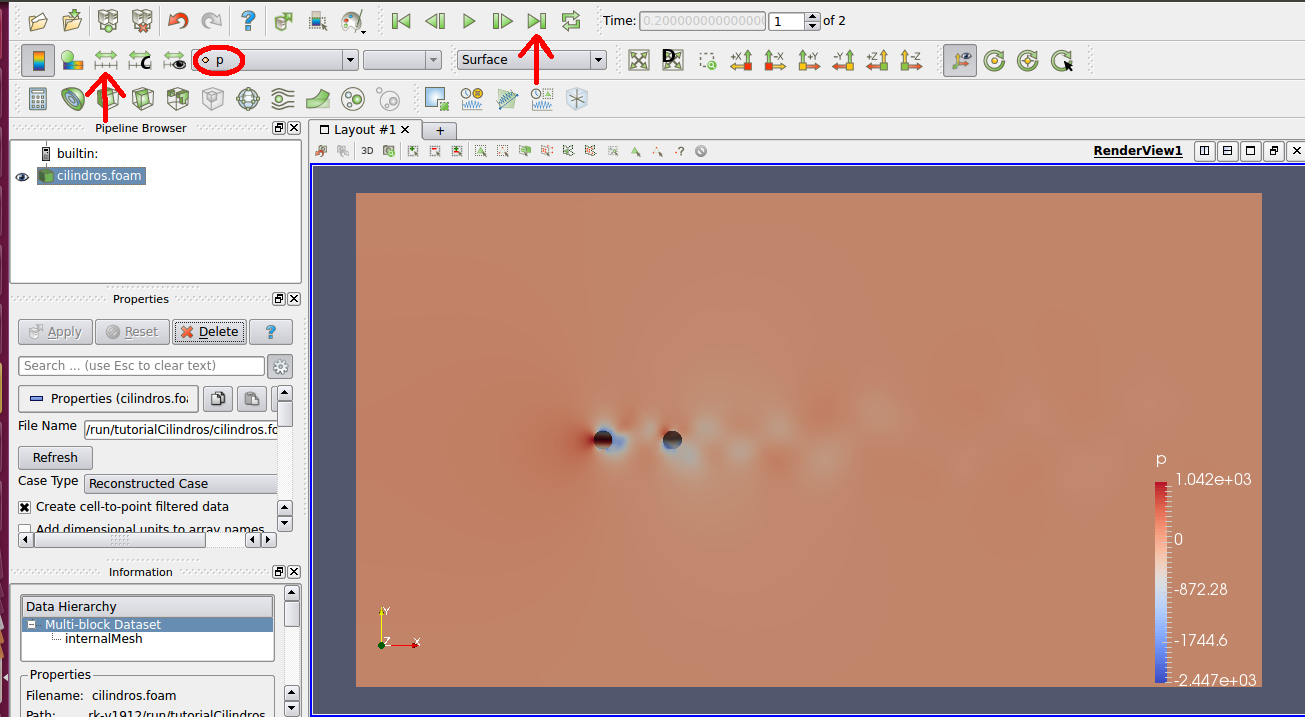
Já o campo de velocidade tem o seguinte resultado:
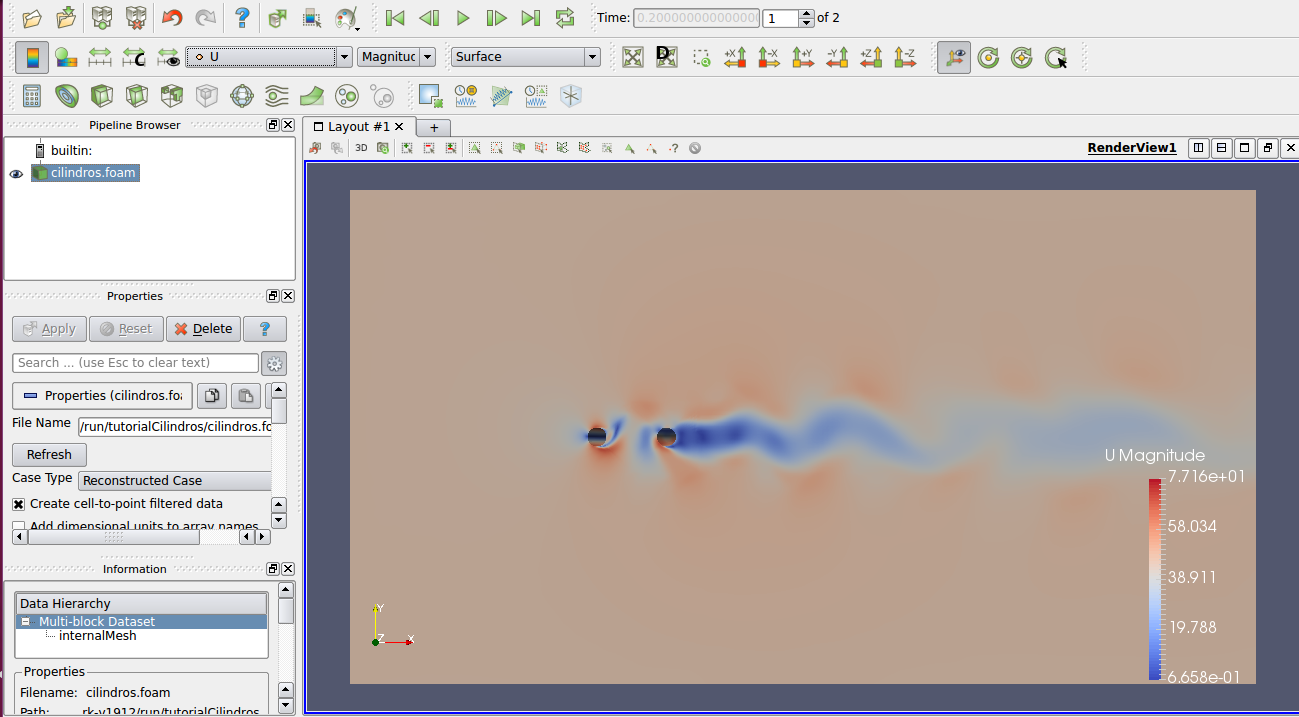
Os dados acústicos encontram-se na pasta “acousticData” dentro da pasta “tutorialCilindros”. Para plotar os gráficos relacionados aos dados acústicos será utilizado aqui um código em Matlab.
Primeiramente é necessário importar os dados. Com o Matlab aberto vá até a aba “Home” e clique em “ImportData”. Vá até o diretório do “tutorialCilindros” e abra a pasta “acousticData”. Vamos plotar os resultados para o microfone A. Selecione então o arquivo “fftCurleAnalogymicrophoneA” e clique em “Open”. Na janela que abrir clique na opção ”ImportSelection”. Repita o mesmo procedimento para abrir os arquivos “fft-superficie1-microphone-A” e “fft-superficie2-microphone-A”.
Para plotar o gráfico comparativo entre os três resultados, isto é, utilizando a analogia de FWH com superfícies 1 e 2, e também utilizando a analogia Curle, é executado o seguinte código:
% Frequências
fCurle = fftCurleAnalogymicrophoneA{:,1};
fS1 = fftsuperficie1microphoneA{:,1};
fS2 = fftsuperficie2microphoneA{:,1};
% Nível de Pressão Sonora
splCurle = fftCurleAnalogymicrophoneA{:,3};
splS1 = fftsuperficie1microphoneA{:,3};
splS2 = fftsuperficie2microphoneA{:,3};
% Espectro de frequência
semilogx(fCurle,splCurle,’-r’)
hold on
semilogx(fS1,splS1,’-b’)
hold on
semilogx(fS2,splS2,’-k’)
hold on
xlabel(“Frequência (Hz)”)
ylabel(“NPS (dB)”)
xlim([50 500])
legend(“Curle”, “FWH-S1”, “FWH-S2”)
Dessa forma, o resultado obtido é:
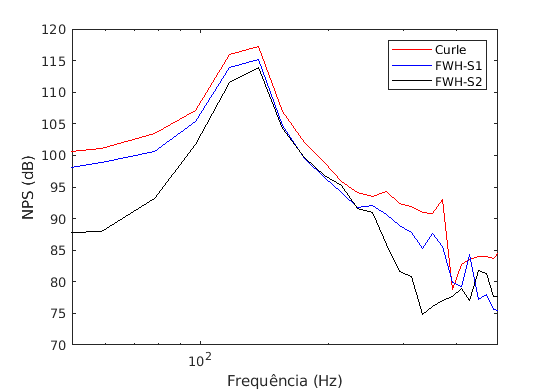
Obs: Para obter melhores resultados pode-se aumentar o número de pontos por bloco da FFT (nfft), tanto no arquivo “fwhCommonSettings” quanto no arquivo “curleControl”. Porém ao aumentar o nfft também pode ser necessário aumentar o tempo de simulação. Vale ressaltar, ainda, que a malha utilizada tem fins meramente didáticos e que se o objetivo for obter resultados próximos de valores experimentais, refinamentos no modelo de simulação devem ser aplicados.