Simulação de um dipolo 3D no OpenFOAM utilizando a biblioteca libAcoustics
Simulação de um dipolo 3D no OpenFOAM utilizando a biblioteca libAcoustics
Observações:
- Este tutorial tem função meramente didática, visando auxiliar usuários iniciantes, e não representa garantias de qualidade de resultados da simulação. A verificação e validação dos resultados, assim como estudos de refino de malha e demais análises, são de responsabilidade do usuário final.
- This offering is not approved or endorsed by OpenCFD Limited, producer and distributor of the OpenFOAM software via www.openfoam.com, and owner of the OPENFOAM® and OpenCFD® trade marks.
- Este tutorial foi criado dentro do contexto de um projeto de extensão da UFSC e não é homologado pelos desenvolvedores dos códigos GMSH, LibAcoustics e OpenFOAM®.
- Foi utilizada a versão 1912 do OpenFOAM.
- Este tutorial foi elaborado pelo aluno de graduação Julio Victor Vieira, sob supervisão de Filipe Dutra da Silva.
- Ao utilizar este material, solicita-se que sejam dadas as devidas referências à esta página. Dúvidas e sugestões podem ser enviadas aos endereços de contato da página.
Este tutorial tem o objetivo de mostrar algumas funcionalidades da biblioteca de acústica libAcoustics criada por Epikhin et al. para OpenFOAM, utilizando um caso de dipolo 3D. Esta biblioteca contém a implementação de analogias acústicas que permitem o cálculo do ruído em campo distante a partir de dados coletados próximos à fonte. Aqui faremos o uso da analogia de Ffowcs Williams-Hawkings.
Primeiramente é calculada a pressão acústica no domínio do tempo. Em seguida, esses dados são convertidos para o domínio da frequência utilizando o algoritmo Fast Fourier Transform (FFT).
Obs: Antes de instalar a biblioteca libAcoustics, é necessário ter instalado a biblioteca FFTW.
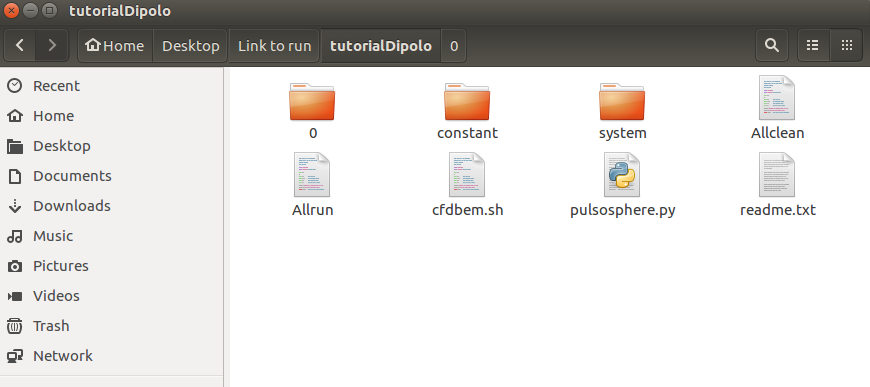
Para começar, copie o caso “monopole3D” presente na pasta “Tutorials” que acompanha os arquivos de instalação da biblioteca e cole no diretório desejado com o nome “tutorialDipolo”. A pasta deve conter os seguintes arquivos:
Abra a pasta “system” e em seguida o arquivo “controlDict”. Vamos utilizar o solver “rhoPimpleFoam”. Mude o valor de “deltaT” para 2.5e-4, o valor de “endTime” para 0.13, e o valor de “maxDeltaT” para 1e-3, conforme mostrado abaixo. As funções inseridas pertencem à biblioteca libAcoustics.
application rhoPimpleFoam;
startFrom startTime;
startTime 0;
stopAt endTime;
endTime 0.13;
deltaT 2.5e-4;
writeControl adjustableRunTime;
writeInterval 5e-3;
purgeWrite 200;
writeFormat ascii;
writePrecision 9;
writeCompression on;
timeFormat general;
timePrecision 6;
runTimeModifiable true;
adjustTimeStep false;
maxCo 0.5;
maxDeltaT 1e-3;
functions
{
#include "probeControl"
#include "fwhControl"
#include "sphereAverage"
#include "soundPressureSampling"
}
Após aplicar as mudanças necessárias, salve-as e feche o arquivo. Em seguida, abra o arquivo “fwhCommonSettings”. Nele estão contidas as configurações da analogia acústica utilizada, conhecida como Ffowcs Williams-Hawkings (FWH). Altere o “timeStart” para 0.001. Modifique a velocidade de propagação (c0) e a densidade (rhoInf) para os valores referentes ao ar, conforme indicado abaixo. O “dRef” é utilizado em simulações 2D para definir a espessura do domínio, mas como nosso caso é 3D altere o valor para -1 para ignorar essa função. As posições no campo distante onde se deseja fazer as medições do ruído devem ser configuradas em “observers”.
libs (“libAcoustics.so”);
log true;
writeFft true;
probeFrequency 1;
timeStart 0.001;
timeEnd 0.13;
c0 340;
dRef -1;
pName p;
pInf 101325;
rho rho;
rhoInf 1.22;
CofR (0 0 0);
observers
{
R-A
{
position (0 0 1.0);
pRef 2.0e-5;
fftFreq 512;
}
R-B
{
position (0 0 2.0);
pRef 2.0e-5;
fftFreq 512;
}
R-C
{
position (0 0 3.0);
pRef 2.0e-5;
fftFreq 512;
}
R-D
{
position (0 0 4.0);
pRef 2.0e-5;
fftFreq 512;
}
R-E
{
position (0 0 5.0);
pRef 2.0e-5;
fftFreq 512;
}
R-F
{
position (0 0 10.0);
pRef 2.0e-5;
fftFreq 512;
}
}
No arquivo “fwhControl” constam as configurações das superfícies que coletam os dados nas regiões próximas da fonte. Utilizaremos as mesmas superfícies do caso do monopolo. Estas superfícies envolvem toda a esfera. Elas estão localizadas na pasta constant/triSurface e devem ter o formato .stl.
No arquivo “decomposeParDict” mude o valor de “numberOfSubdomains” para quantidade de processadores que você deseja utilizar na simulação em paralelo.
Os demais arquivos da pasta “system” não serão alterados. Agora saia da pasta “system” e entre na pasta “constant”. Abra o arquivo “thermophysicalProperties” e modifique os valores conforme mostrado abaixo. Feito isso, salve o arquivo e feche-o. Ainda dentro da pasta “constant” altere o nome da pasta “polyMesh0” para “polyMesh” (apenas retire o “0”).
thermoType
{
type hePsiThermo;
mixture pureMixture;
transport const;
thermo hConst;
equationOfState perfectGas;
specie specie;
energy sensibleEnthalpy;
}
mixture
{
specie
{
nMoles 1;
molWeight 28.9;
}
thermodynamics
{
Cp 1005;
Hf 0;
}
transport
{
mu 1.8e-05;
Pr 0.7;
}
}
O próximo passo é configurar as condições de contorno. Saia da pasta “constant” e abra a pasta “0” e em seguida abra o arquivo “U”. É aqui que vamos alterar a configuração de um monopolo para a configuração de um dipolo. Podemos definir um dipolo como um monopolo que oscila em uma única direção. Para fazer isso, altere as configurações de “sphere” para as que aparecem logo abaixo.
dimensions [0 1 -1 0 0 0 0];
internalField uniform (0 0 0);
boundaryField
{
free
{
type waveTransmissive;
field U;
phi phi;
rho rho;
psi thermo:psi;
gamma 1.4;
value uniform (0 0 0);
}
sphere
{
type uniformFixedValue;
uniformValue sine;
uniformValueCoeffs
{
amplitude 0.01;
scale (0 0 1);
level (0 0 0);
frequency constant 100;
}
}
#include "cyc"
}
Observação: A condição de contorno “waveTransmissive” presente em “free” é utilizada para evitar a reflexão das ondas nas fronteiras do domínio computacional.
As demais condições de contorno são mantidas iguais às do caso do monopolo.
Com as configurações do caso prontas, abra o terminal e vá até a pasta “tutorialDipolo” digite “decomposePar” e aperte enter para fazer a divisão do domínio, já que vamos rodar a simulação em paralelo.

Assim, já podemos começar a rodar a simulação. Para isso digite “mpirun -np 5 rhoPimpleFoam -parallel > log &” e aperte enter (substitua o número 5 pelo número de processadores que você configurou no arquivo “decomposeParDict”).

Pós-processamento
Após terminar a simulação, vá até o terminal e digite “reconstructPar -latestTime” para reconstruir o último passo de tempo da simulação.

Depois, vamos criar um arquivo que possa ser lido no Paraview. Para isso, digite “nano dipolo.foam”, então pressione “enter”, depois ctrl+o, “enter” e por fim ctrl+x.

Digite “paraview dipolo.foam” para visualizar o resultado no Paraview.

Clique em avançar para o último passo de tempo e depois desmarque a opção “internalMesh” na barra à esquerda e marque a opção “sphere”, como indicado na imagem abaixo. Clique em “Apply” para visualizar o resultado.
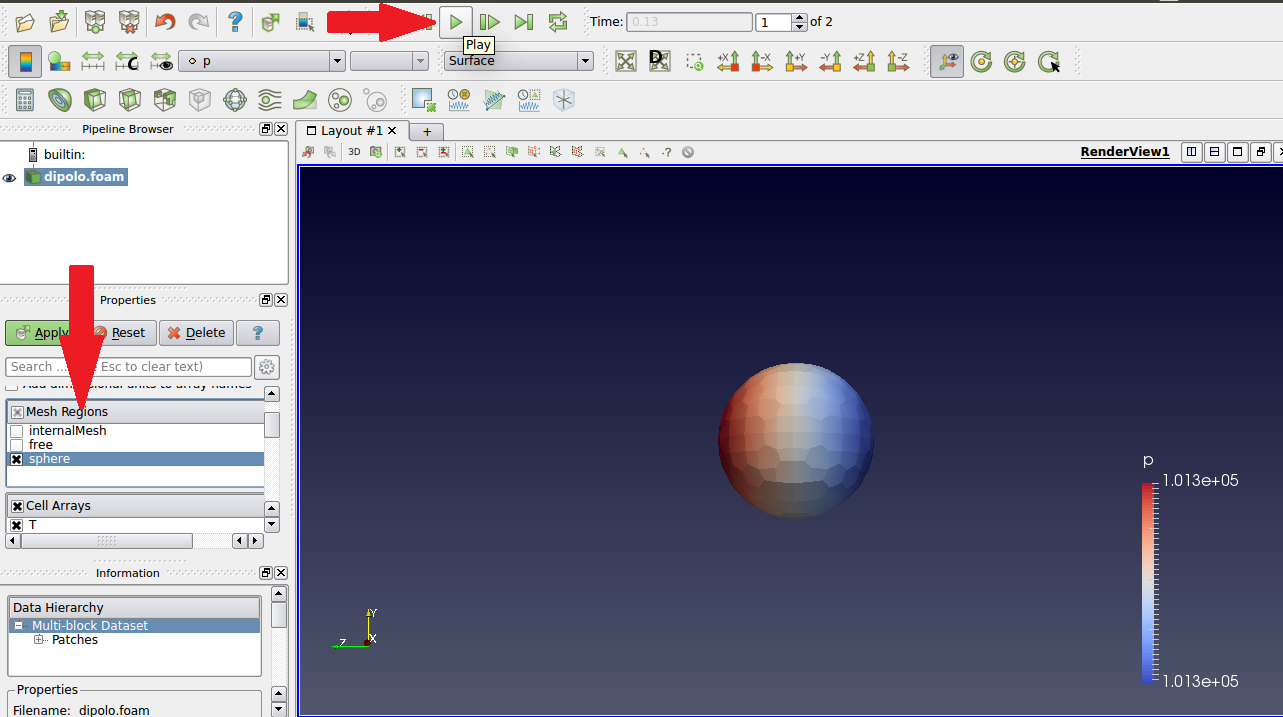
Os dados da simulação acústica são salvos na pasta “acousticData” dentro da pasta “tutorialDipolo”. Aqui será apresentado um código em Matlab que plota os resultados da pressão acústica em função do tempo e também o espectro de frequência para o microfone A.
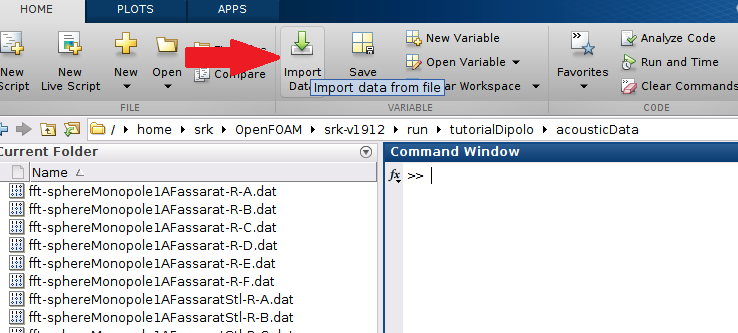
Primeiro, clique na opção “Import Data” conforme mostrado abaixo e selecione o arquivo “fft-sphereMonopole1AFassaratStl-R-A.dat”. Na janela que abrir clique em “Import Selection”. Faça o mesmo procedimento para importar o arquivo “sphereMonopole1AFassarat-time.dat”.
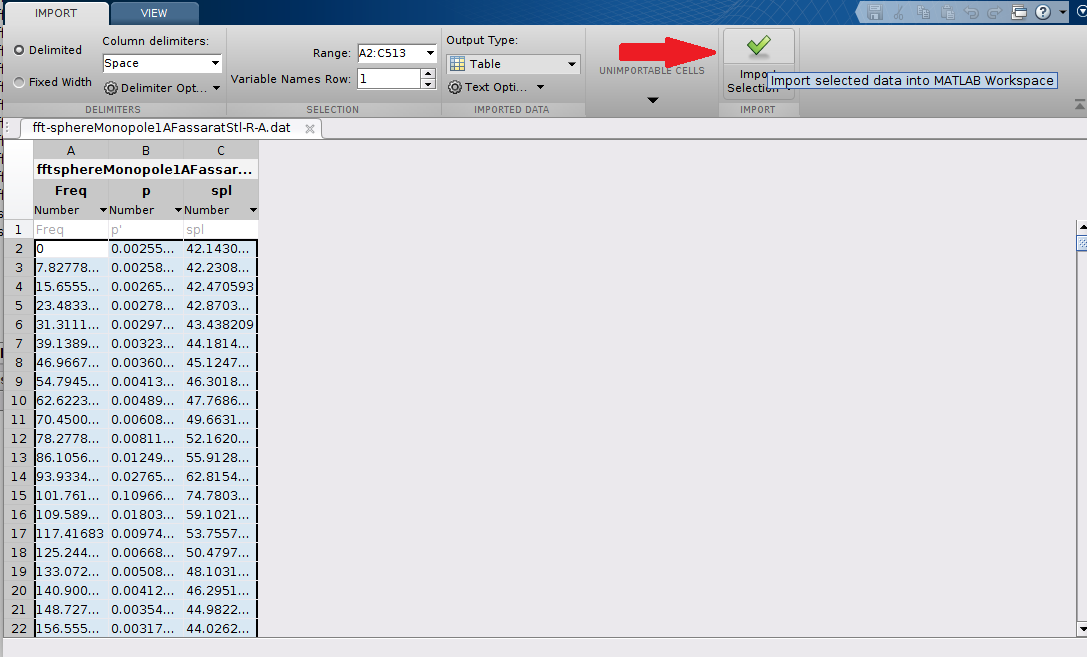
Para plotar os gráficos, basta executar o seguinte script:
t = sphereMonopole1AFassaratStltime{:,1};
p = sphereMonopole1AFassaratStltime{:,2};
f = fftsphereMonopole1AFassaratStlRA{1:256,1};
spl = fftsphereMonopole1AFassaratStlRA{1:256,3};
figure(1)
plot(t,p)
xlabel(“Tempo(s)”)
ylabel(“Pressão Acústica (Pa)”)
figure(2)
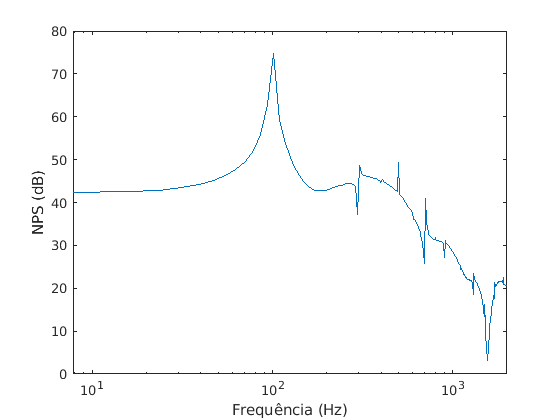
semilogx(f,spl)
xlabel(“Frequência (Hz)”)
ylabel(“NPS (dB)”)
Pressão acústica em função do tempo:
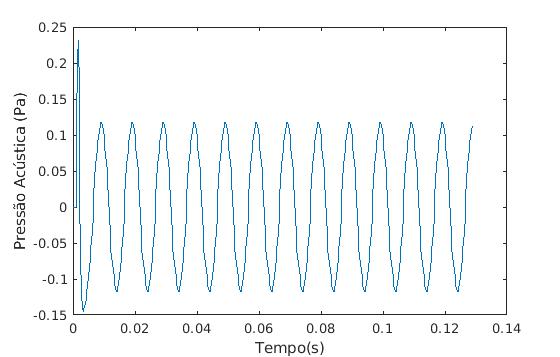
Espectro de frequência: